Le génie stratégique de la nature : pourquoi les cerfs ne se battent-ils pas à mort ?

Jusqu'au milieu du XXe siècle, cette question d'apparence simple était une véritable énigme pour les biologistes. La réponse naïve — selon laquelle les animaux se retiendraient « pour le bien de l'espèce » — s'est avérée scientifiquement intenable. L'évolution opère au niveau du succès individuel, et non pour un vague « bien commun ». Un individu qui se battrait jusqu'à la mort et gagnerait serait, en théorie, plus apte à transmettre ses gènes. Alors, pourquoi cette stratégie de tueur ne s'est-elle pas davantage répandue ?

La réponse est venue d'un biologiste britannique nommé John Maynard Smith, qui a créé un tout nouveau champ d'étude : la théorie des jeux évolutionniste. Son travail a changé à jamais notre vision de l'évolution du comportement et a introduit l'un des concepts les plus importants de la biologie : la Stratégie Évolutivement Stable (SES).

Le problème : les animaux ne jouent pas aux échecs

La théorie des jeux a été initialement développée par des économistes et des mathématiciens pour modéliser les décisions d'agents rationnels et calculateurs — des personnes, des entreprises ou des pays — qui planifient consciemment l'avenir. Mais les animaux ne sont pas comme ça. Un cerf n'effectue pas de calculs de probabilités complexes avant un combat. Son comportement est largement guidé par des instincts et des stratégies génétiquement codés.

La brillante intuition de John Maynard Smith fut que la logique de la théorie des jeux pouvait parfaitement s'appliquer à l'évolution si l'on changeait simplement les termes :

• Les joueurs ne sont pas des individus conscients mais les membres d'une population.
• Les stratégies ne sont pas des choix délibérés mais des comportements déterminés génétiquement (par ex., « toujours se battre », « toujours battre en retraite »).
• Le gain n'est pas de l'argent mais le succès reproductif, ou la valeur sélective (fitness) — un terme qui, dans ce contexte évolutif, ne se réfère pas à la force physique, mais simplement à la probabilité de transmettre ses gènes.

Dans ce cadre, la question centrale devient : quelle stratégie comportementale peut persister et se propager dans une population sur le long terme, surtout lorsqu'elle est en compétition avec d'autres stratégies ?

La solution : la Stratégie Évolutivement Stable (SES)

Maynard Smith a défini une stratégie comme étant évolutivement stable si, dans une population où presque tout le monde l'adopte, aucune stratégie alternative (ou « mutante ») ne peut réussir à l'envahir.

Imaginez une stratégie établie et performante comme un roi au sommet d'une colline. Une SES est un « roi » capable de résister à toute rébellion à petite échelle. Si un individu mutant avec un comportement différent apparaît dans la population, il aura simplement de moins bons résultats que les autres, et sa descendance ne se propagera pas. Une SES est donc une stratégie « à l'épreuve des invasions ».

La définition mathématique formelle comporte deux conditions :

1. Une SES doit obtenir de meilleurs résultats contre elle-même que n'importe quelle stratégie mutante contre la SES. (C'est le cas simple : le mutant est immédiatement désavantagé.)
2. Si un mutant obtient des résultats aussi bons contre la SES que la SES contre elle-même, alors la SES doit obtenir de meilleurs résultats contre le mutant que le mutant contre lui-même. (C'est une règle de « départage » qui empêche un mutant neutre de se propager par dérive génétique aléatoire.)

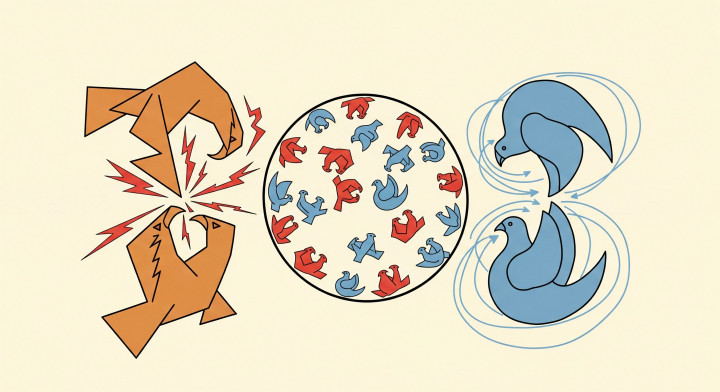
L'exemple classique : le jeu du faucon et de la colombe

Pour comprendre la logique d'une SES, examinons le modèle le plus célèbre de Maynard Smith : le jeu du faucon et de la colombe. Imaginez une population où les conflits pour une ressource peuvent être gérés de deux manières :

• Faucon : Se bat toujours, de manière agressive et en escaladant le conflit. S'il gagne, il obtient le prix. S'il perd, il subit une grave blessure.
• Colombe : Ne se bat jamais. Elle se contente de parader et de prendre des postures. Si son adversaire attaque, elle s'enfuit immédiatement, évitant la blessure.

Analysons ce qui se passerait :

1. Un monde de colombes : Dans une population composée uniquement de colombes, les conflits sont pacifiques. Les individus paradent, et la ressource est souvent partagée. C'est un monde paisible mais vulnérable. Si un seul mutant Faucon apparaît, c'est le paradis pour lui. Il peut intimider chaque colombe sans combattre et s'approprier toutes les ressources. La stratégie Faucon se répandrait comme une traînée de poudre. Par conséquent, une stratégie « pure Colombe » n'est pas une SES.
2. Un monde de faucons : Dans une population composée uniquement de faucons, chaque conflit débouche sur un combat brutal. Les gagnants raflent tout, mais les perdants sont gravement blessés, ce qui réduit considérablement leurs chances de reproduction. Si le coût de la blessure (C) est supérieur à la valeur du prix (V), le gain moyen pour un faucon est négatif. Maintenant, si un seul mutant Colombe apparaît dans ce monde sanglant, il ne se battra jamais, donc il ne sera jamais blessé. Bien qu'il perde chaque confrontation contre un faucon, son gain de zéro est toujours meilleur que le gain moyen négatif des faucons. La stratégie Colombe peut réussir à envahir la population. Par conséquent, une stratégie « pur Faucon » n'est pas une SES.

Quelle est donc la solution ? Dans ce cas, la SES n'est pas une stratégie pure mais une stratégie mixte. La population se stabilise dans un état avec une certaine proportion de faucons et de colombes. Ce ratio est déterminé par la valeur du prix et le coût de la blessure. À ce point d'équilibre, le succès reproductif moyen d'un faucon est exactement égal à celui d'une colombe, de sorte qu'aucun ne peut surpasser l'autre.

Cela explique le comportement des cerfs. La plupart des espèces suivent une stratégie mixte où certains conflits n'impliquent que des postures ritualisées (comportement de type Colombe), et seules certaines situations dégénèrent en combat réellement dangereux (comportement de type Faucon).

Conclusion : La logique de l'évolution comportementale

Les travaux de John Maynard Smith ont fondamentalement changé la biologie. Le concept de SES a donné aux chercheurs un puissant outil mathématique pour analyser la logique du comportement au niveau de l'avantage individuel. Il a remplacé les explications vagues basées sur la sélection de groupe et a montré que les comportements stables que nous observons dans la nature — de l'agression à l'altruisme — sont le résultat d'un équilibre stratégique sous-jacent.

Aujourd'hui, la théorie des jeux évolutionniste n'est pas seulement utilisée pour étudier le comportement animal, mais elle est aussi un outil fondamental en économie, en sociologie, et même dans la recherche sur le cancer et les virus. Elle nous aide à comprendre que la « lutte pour la survie » n'est pas toujours une question de victoire du plus fort ou du plus agressif. C'est un jeu complexe et dynamique où les stratégies les plus « à l'épreuve des invasions », les plus évolutivement stables, sont celles qui persistent — créant ainsi la diversité comportementale merveilleuse et parfois déconcertante que nous observons dans le monde naturel.