El Desarrollo del Backpropagation

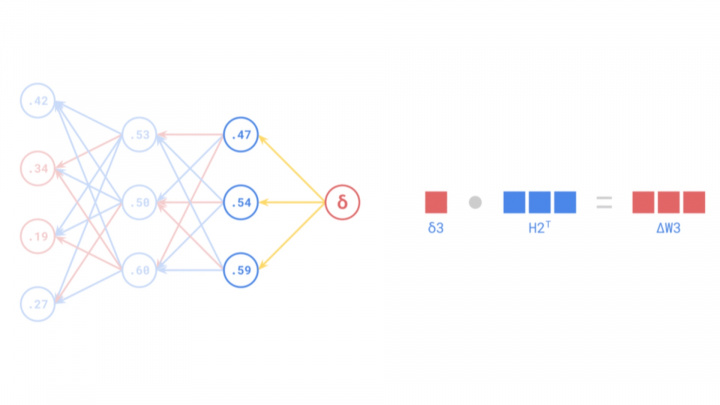
Aunque es una herramienta indispensable en la inteligencia artificial moderna y el aprendizaje automático, la historia de backpropagation abarca varias décadas e involucra numerosos avances científicos. Su desarrollo comenzó conceptualmente en la década de 1960, pero solo ganó prominencia generalizada a mediados de la década de 1980 tras las contribuciones fundamentales y la popularización por parte de investigadores como Frank Rosenblatt, Seppo Linnainmaa y Paul Werbos.

Primeros Fundamentos Teóricos

Los fundamentos teóricos de backpropagation surgieron ya en la década de 1960 a través del trabajo de varios investigadores en diferentes campos. Una contribución temprana y conceptualmente relacionada provino de Frank Rosenblatt, conocido por desarrollar el Perceptrón, un modelo simple de una red neuronal. En 1962, describió un procedimiento de "corrección de errores por retropropagación" para sus ideas de perceptrón multicapa. Si bien el perceptrón monocapa tenía limitaciones (famosamente incapaz de resolver el problema XOR), y su corrección de errores específica no era el backpropagation general que usamos hoy en día, el trabajo de Rosenblatt sentó las bases para desarrollos posteriores en redes multicapa.

Simultáneamente, en el campo de la teoría de control y la optimización, los investigadores estaban desarrollando métodos basados en la regla de la cadena para calcular gradientes. Henry J. Kelley, en 1960, propuso un método donde los gradientes se propagaban hacia atrás a través de un grafo computacional que representaba un proceso de control. Stuart Dreyfus publicó una derivación más simple basada en la regla de la cadena en 1962. Si bien no se aplicaron directamente a las redes neuronales en ese momento, estos principios de cálculo eficiente de derivadas mediante la propagación de información hacia atrás fueron precursores cruciales del backpropagation moderno.

Sin embargo, en la década de 1960, el campo de las redes neuronales aún era incipiente y los recursos computacionales necesarios para implementar algoritmos complejos de manera efectiva eran escasos. No obstante, los investigadores en teoría de control y optimización continuaron refinando estos principios, lo que finalmente condujo a la forma moderna del algoritmo de backpropagation.

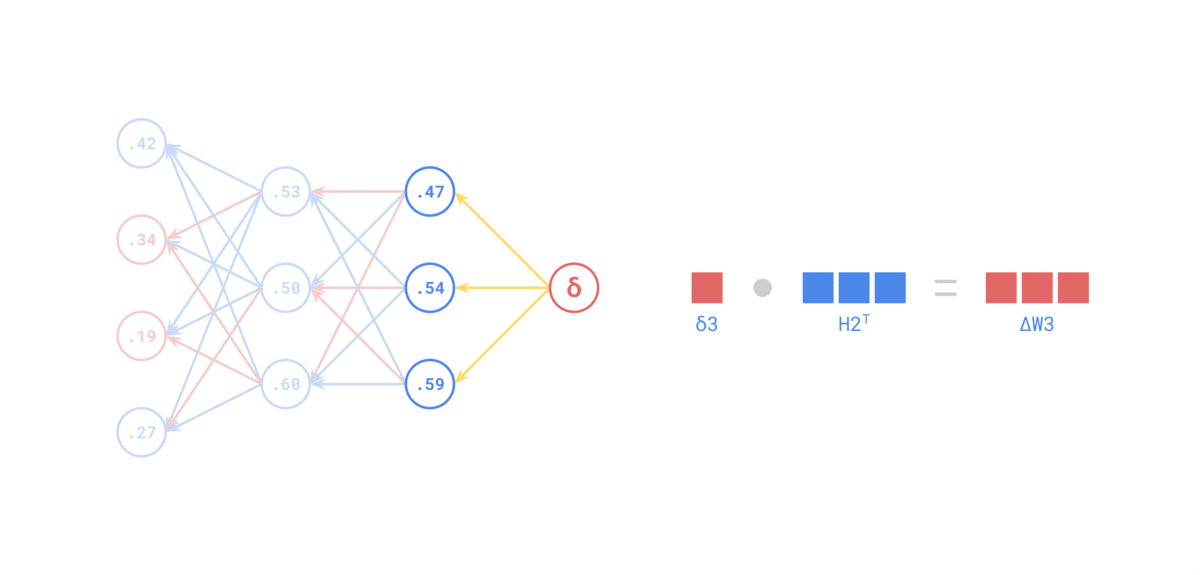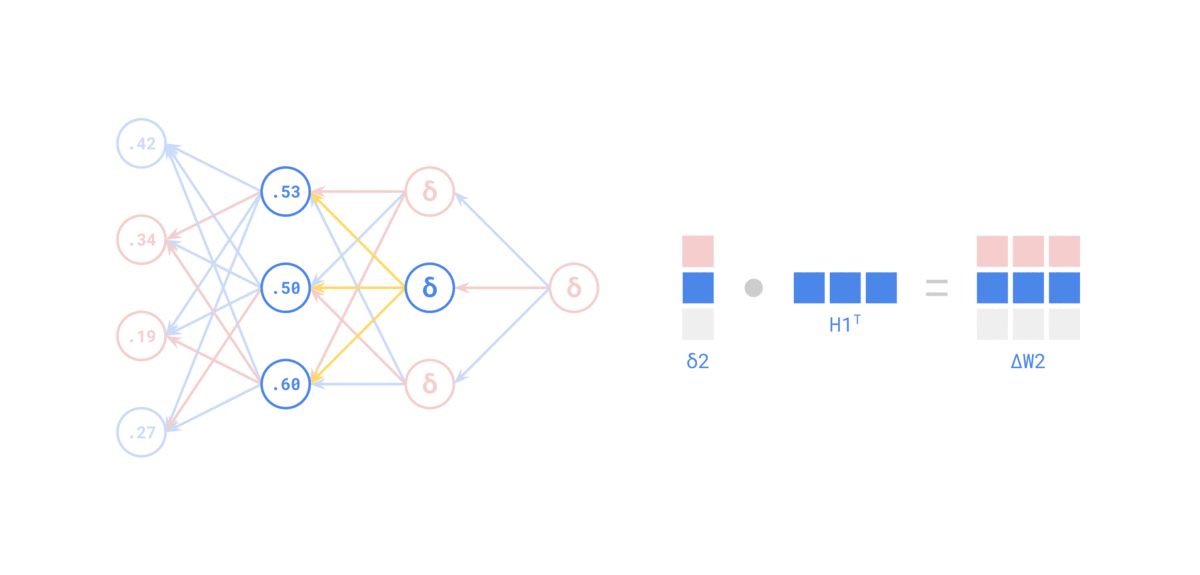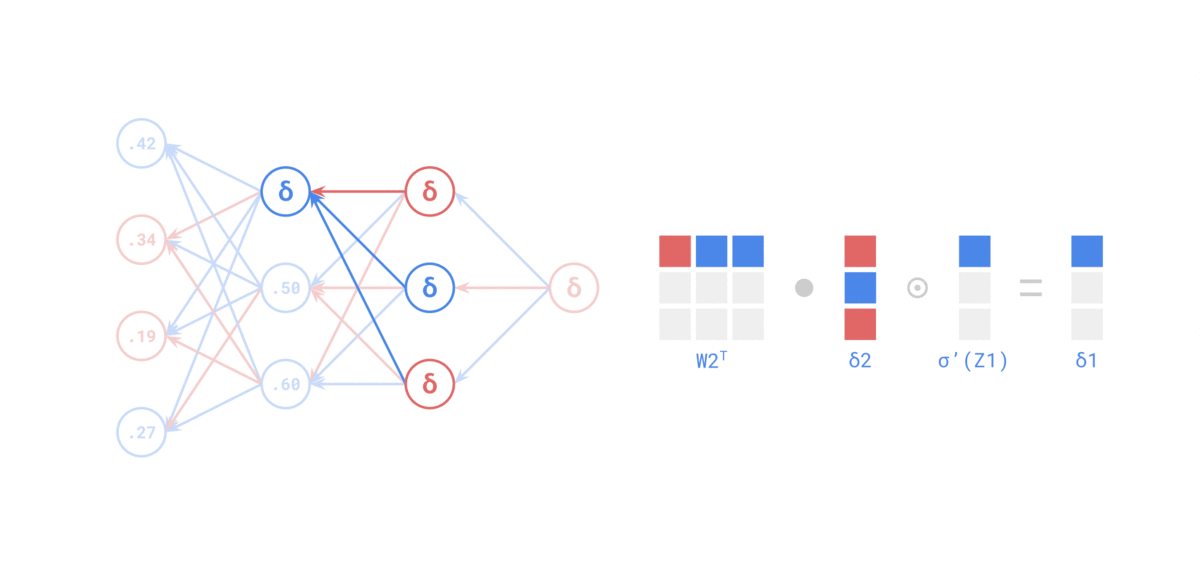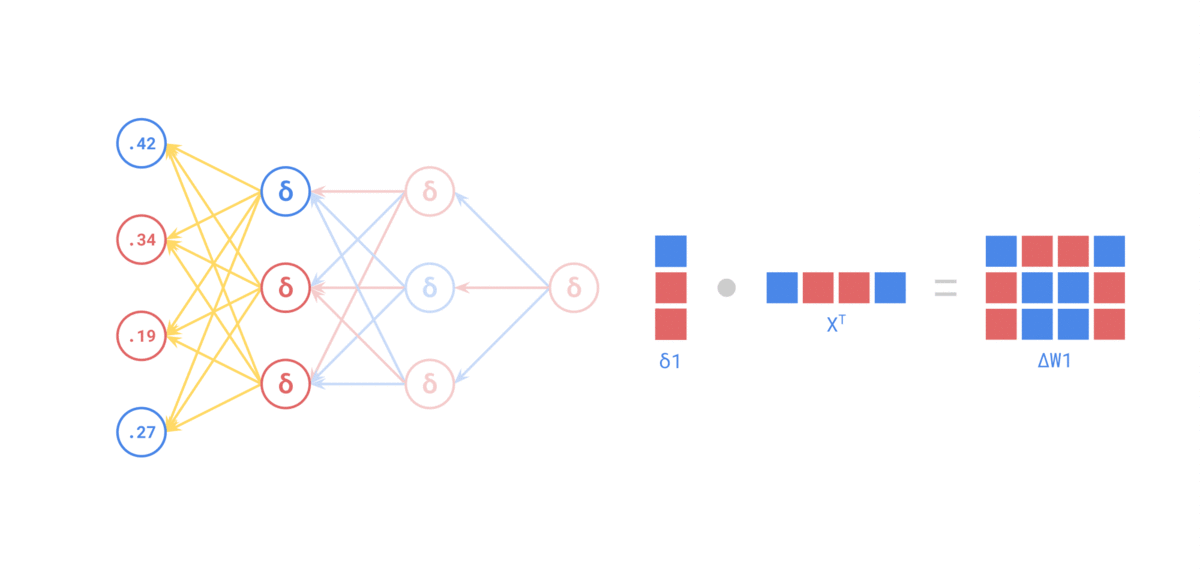
Fuente: https://medium.com/the-feynman-journal/what-makes-backpropagation-so-elegant-657f3afbbd

Formalización y Popularización

La forma moderna y eficiente del algoritmo, conocida como diferenciación automática en modo inverso, fue descrita rigurosamente por el investigador finlandés Seppo Linnainmaa en su tesis de maestría de 1970 (publicada en 1976). Linnainmaa desarrolló este método general para calcular eficientemente las derivadas de funciones complejas y anidadas, que constituye el núcleo matemático del backpropagation actual. Sin embargo, el trabajo de Linnainmaa no se centró en las redes neuronales.

La conexión crucial con las redes neuronales fue explicitada por Paul Werbos en su tesis doctoral de 1974 (publicada posteriormente). Werbos reconoció que la diferenciación automática en modo inverso de Linnainmaa podría aplicarse para entrenar redes neuronales artificiales multicapa. Primero demostró cómo este algoritmo podía ajustar eficientemente los pesos en perceptrones multicapa (PMC), superando las limitaciones de los perceptrones monocapa y permitiendo que las redes aprendieran patrones complejos. El trabajo de Werbos fue un avance en el campo de la IA, allanando el camino para futuros avances en redes neuronales.

A pesar de estos desarrollos, el algoritmo de backpropagation no ganó atención generalizada hasta mediados de la década de 1980. En 1986, David E. Rumelhart, Geoffrey Hinton y Ronald J. Williams publicaron su artículo fundamental, "Learning representations by back-propagating errors" (Aprendizaje de representaciones mediante retropropagación de errores). Este artículo demostró claramente el poder práctico de backpropagation para entrenar PMC en diversos problemas. El estudio fue de importancia crítica porque mostró de manera convincente que las RNA podían aprender representaciones internas útiles y resolver tareas complejas que antes se consideraban intratables para ellas. El artículo jugó un papel clave no solo en la popularización del algoritmo, sino también en la revitalización de la investigación en redes neuronales, que había enfrentado escepticismo durante el anterior "invierno de la IA".

Este artículo histórico reavivó el interés en las RNA dentro de la comunidad de investigación de IA. Gracias a la eficiencia de backpropagation, las redes multicapa se volvieron efectivamente entrenables, abriendo la puerta a la revolución del aprendizaje profundo y a los principales avances en la inteligencia artificial moderna.

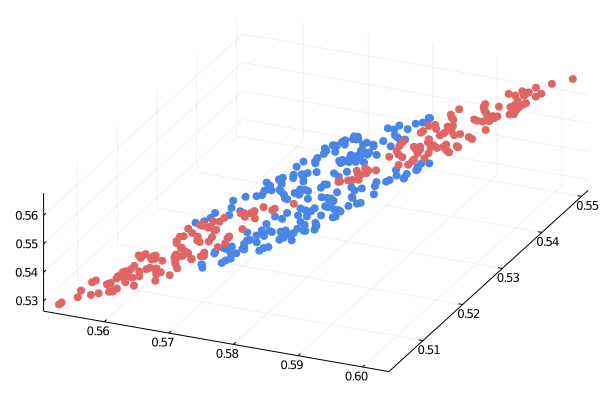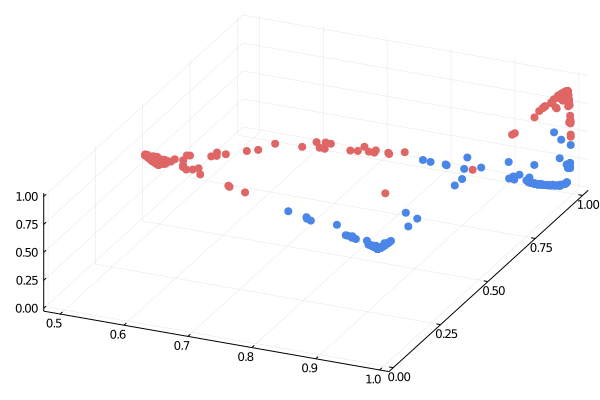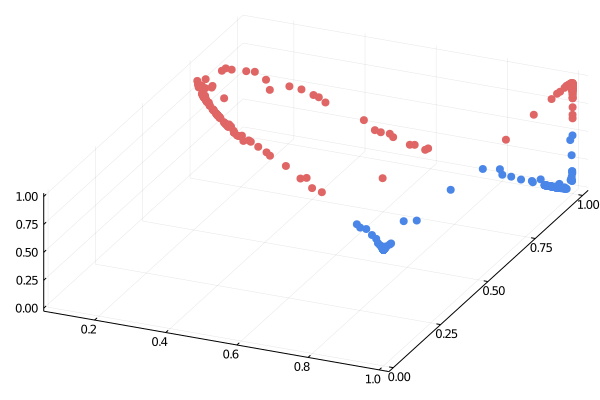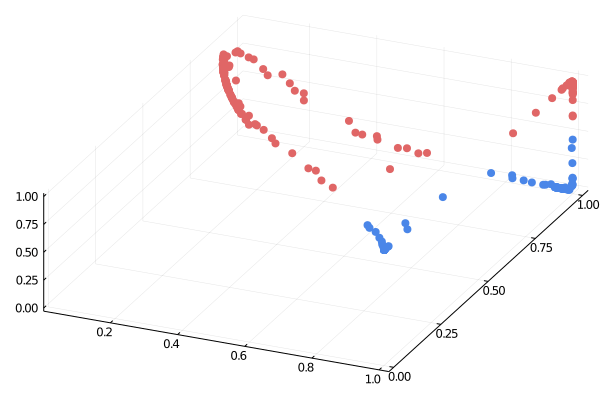
Fuente: https://medium.com/the-feynman-journal/what-makes-backpropagation-so-elegant-657f3afbbd

Aplicaciones Prácticas: El Avance de Yann LeCun

Aunque los fundamentos teóricos de backpropagation se establecieron en las décadas de 1960 y 1970, su primera aplicación práctica verdaderamente impactante surgió a finales de la década de 1980. Yann LeCun, ahora reconocido como uno de los pioneros de la IA, demostró el poder de combinar backpropagation con Redes Neuronales Convolucionales (CNN) mientras trabajaba en Bell Labs en 1989. LeCun y sus colegas aplicaron CNN entrenadas con backpropagation a la tarea de reconocimiento de dígitos manuscritos.

Esta aplicación revolucionaria condujo al desarrollo de un sistema capaz de leer automáticamente dígitos manuscritos en cheques. El trabajo de LeCun no solo demostró que backpropagation podía resolver problemas complejos del mundo real, sino que también mostró que las redes neuronales, particularmente las arquitecturas CNN, eran altamente efectivas para tareas de visión por computador. Este avance marcó el comienzo de una nueva era en la IA, allanando el camino para el uso generalizado de redes neuronales y backpropagation en numerosas aplicaciones industriales y de investigación.

El trabajo de LeCun fue particularmente significativo porque las CNN son muy adecuadas para procesar datos visuales, ya que pueden capturar las jerarquías espaciales en las imágenes. Backpropagation permitió que estas redes aprendieran los pesos de filtro apropiados para minimizar los errores de clasificación, permitiendo la extracción eficiente de características significativas de los datos de imagen.

El nombre de Yann LeCun se ha vuelto sinónimo de CNN y aprendizaje profundo. En 2018, él, junto con Geoffrey Hinton y Yoshua Bengio, recibió el Premio Turing, el máximo honor en informática, por sus contribuciones fundamentales al aprendizaje profundo. El trabajo de LeCun proporcionó un puente crucial desde la teoría de backpropagation hasta aplicaciones prácticas poderosas, abriendo nuevos horizontes para la inteligencia artificial.

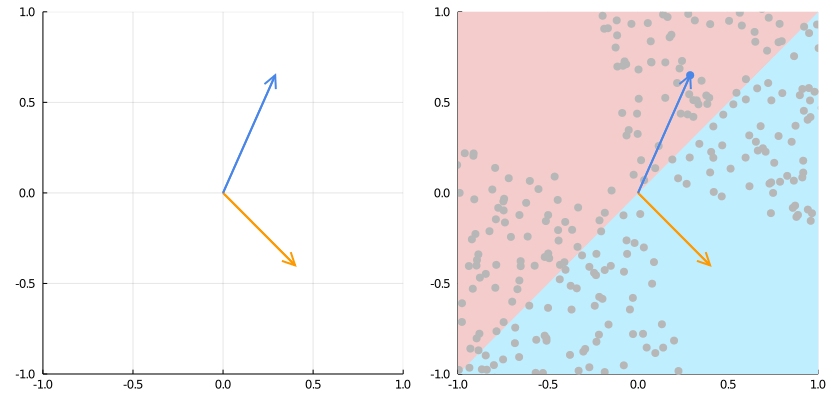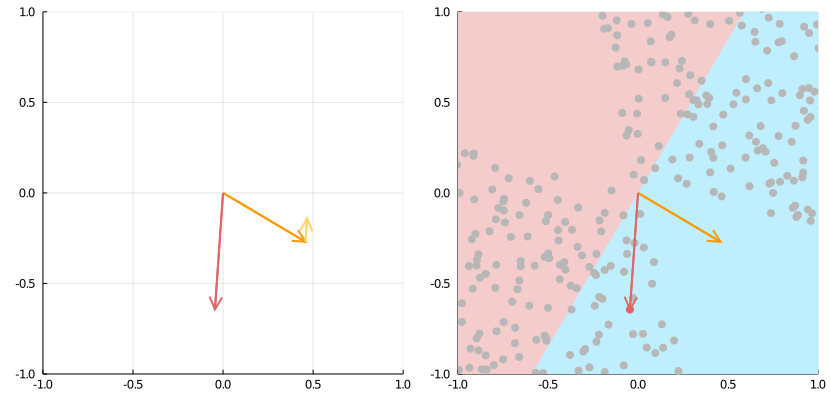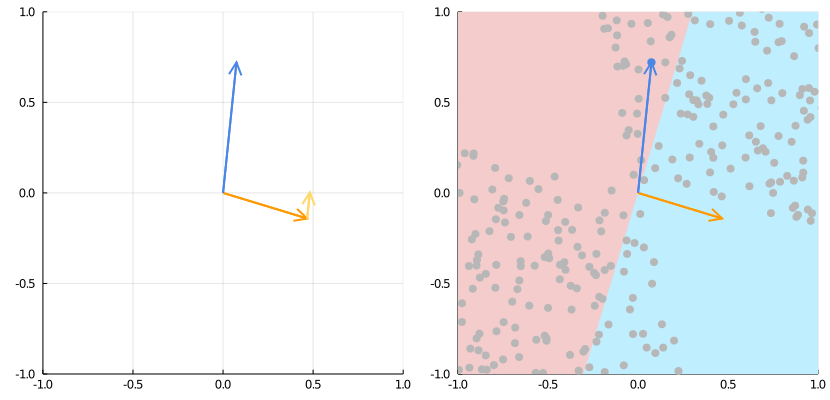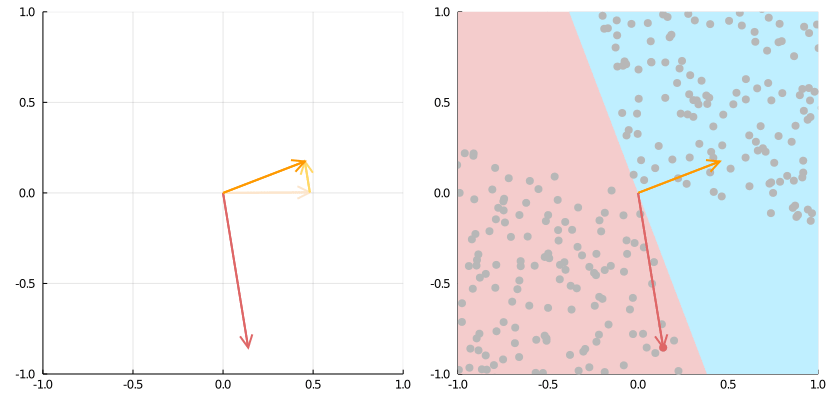
Fuente: https://medium.com/the-feynman-journal/what-makes-backpropagation-so-elegant-657f3afbbd

Desafíos y Evolución de Backpropagation

A pesar de su adopción generalizada y utilidad probada, backpropagation no estuvo exento de desafíos, especialmente a medida que los investigadores comenzaron a construir redes más profundas. Surgieron dos problemas significativos: los problemas del gradiente evanescente y del gradiente explosivo.

El Problema del Gradiente Evanescente

Los gradientes evanescentes ocurren en redes profundas cuando la señal de error disminuye exponencialmente a medida que se propaga hacia atrás desde la capa de salida a las capas anteriores. Durante backpropagation, los gradientes se calculan utilizando la regla de la cadena, que implica multiplicar muchos números pequeños (derivadas de funciones de activación, a menudo menores que 1). En redes profundas, esta multiplicación repetida puede hacer que el gradiente se vuelva extremadamente pequeño, "evanescente". Como resultado, los pesos en las capas anteriores no se actualizan significativamente, lo que dificulta el proceso de aprendizaje. Esto representó un obstáculo importante para entrenar redes neuronales muy profundas.

El Problema del Gradiente Explosivo

Por el contrario, los gradientes explosivos ocurren cuando los gradientes crecen exponencialmente durante backpropagation. Esto puede suceder si los pesos o las derivadas son grandes, lo que lleva a actualizaciones masivas de los pesos. Los pesos de la red pueden divergir rápidamente a valores extremos (como NaN - No es un Número), causando inestabilidad e impidiendo que la red aprenda.

Soluciones y Mejoras

A lo largo de los años, los investigadores desarrollaron numerosas técnicas para mitigar estos problemas de gradiente. Las soluciones clave incluyen:

• Mejores Funciones de Activación: Reemplazar sigmoid/tanh con funciones como ReLU (Unidad Lineal Rectificada) ayudó a aliviar los gradientes evanescentes, ya que la derivada de ReLU es 1 para entradas positivas.
• Esquemas de Inicialización de Pesos: La inicialización cuidadosa de los pesos (por ejemplo, inicialización Xavier/Glorot o He) ayuda a mantener los gradientes en un rango razonable.
• Normalización por Lotes: Esta técnica normaliza las activaciones dentro de las capas intermedias, estabilizando la red y permitiendo tasas de aprendizaje más altas, lo que indirectamente ayuda con los problemas de gradiente.
• Conexiones Residuales (ResNets): Introducidas en las Redes Residuales, estas "conexiones de salto" permiten que los gradientes fluyan más fácilmente a través de la red al omitir algunas capas, combatiendo eficazmente el problema del gradiente evanescente en arquitecturas muy profundas.
• Recorte de Gradiente: Una técnica simple para prevenir los gradientes explosivos limitando los valores del gradiente si exceden un cierto umbral.
• Algoritmos de Optimización Avanzados: Optimizadores como Adam, RMSProp y AdaGrad adaptan la tasa de aprendizaje para cada parámetro, lo que a menudo conduce a una convergencia más rápida y un mejor manejo de paisajes de gradiente desafiantes en comparación con el descenso de gradiente estocástico estándar (SGD).

El Papel de Backpropagation Hoy en Día

Backpropagation sigue siendo uno de los algoritmos más cruciales en el campo del aprendizaje profundo. Aunque han surgido numerosas variaciones y enfoques alternativos, backpropagation (en sus diversas formas, a menudo combinado con las técnicas anteriores) sigue siendo el caballo de batalla para entrenar a la gran mayoría de las redes neuronales. Las RNA modernas han evolucionado hasta convertirse en modelos extremadamente complejos capaces de abordar algunos de los problemas más desafiantes en la IA, incluyendo la visión por computador, el procesamiento del lenguaje natural (PLN) y la conducción autónoma. El algoritmo de backpropagation permitió el desarrollo de estas tecnologías avanzadas y continúa siendo un pilar fundamental del aprendizaje automático.