Le développement de la rétropropagation

Bien qu'elle soit un outil indispensable dans l'intelligence artificielle et l'apprentissage automatique modernes, l'histoire de la rétropropagation s'étend sur plusieurs décennies et implique de nombreuses avancées scientifiques. Son développement a commencé conceptuellement dans les années 1960, mais elle n'a acquis une importance généralisée qu'au milieu des années 1980 après des contributions fondamentales et sa popularisation par des chercheurs tels que Frank Rosenblatt, Seppo Linnainmaa et Paul Werbos.

Premières bases théoriques

Les fondements théoriques de la rétropropagation ont émergé dès les années 1960 grâce aux travaux de divers chercheurs dans différents domaines. Une contribution précoce et conceptuellement liée est venue de Frank Rosenblatt, connu pour avoir développé le Perceptron, un modèle simple de réseau neuronal. En 1962, il a décrit une procédure de "correction d'erreur par rétropropagation" pour ses idées de perceptron multicouche. Bien que le perceptron monocouche ait eu des limitations (notamment son incapacité à résoudre le problème XOR), et que sa correction d'erreur spécifique ne soit pas la rétropropagation générale que nous utilisons aujourd'hui, les travaux de Rosenblatt ont jeté les bases des développements ultérieurs dans les réseaux multicouches.

Simultanément, dans le domaine de la théorie du contrôle et de l'optimisation, des chercheurs développaient des méthodes basées sur la règle de la chaîne pour calculer les gradients. Henry J. Kelley, en 1960, a proposé une méthode où les gradients étaient propagés vers l'arrière à travers un graphe de calcul représentant un processus de contrôle. Stuart Dreyfus a publié une dérivation plus simple basée sur la règle de la chaîne en 1962. Bien que ces principes de calcul efficace des dérivées par propagation d'informations vers l'arrière n'aient pas été directement appliqués aux réseaux neuronaux à l'époque, ils ont été des précurseurs cruciaux de la rétropropagation moderne.

Cependant, dans les années 1960, le domaine des réseaux neuronaux était encore naissant et les ressources de calcul nécessaires pour mettre en œuvre efficacement des algorithmes complexes faisaient défaut. Néanmoins, les chercheurs en théorie du contrôle et en optimisation ont continué à affiner ces principes, ce qui a finalement conduit à la forme moderne de l'algorithme de rétropropagation.

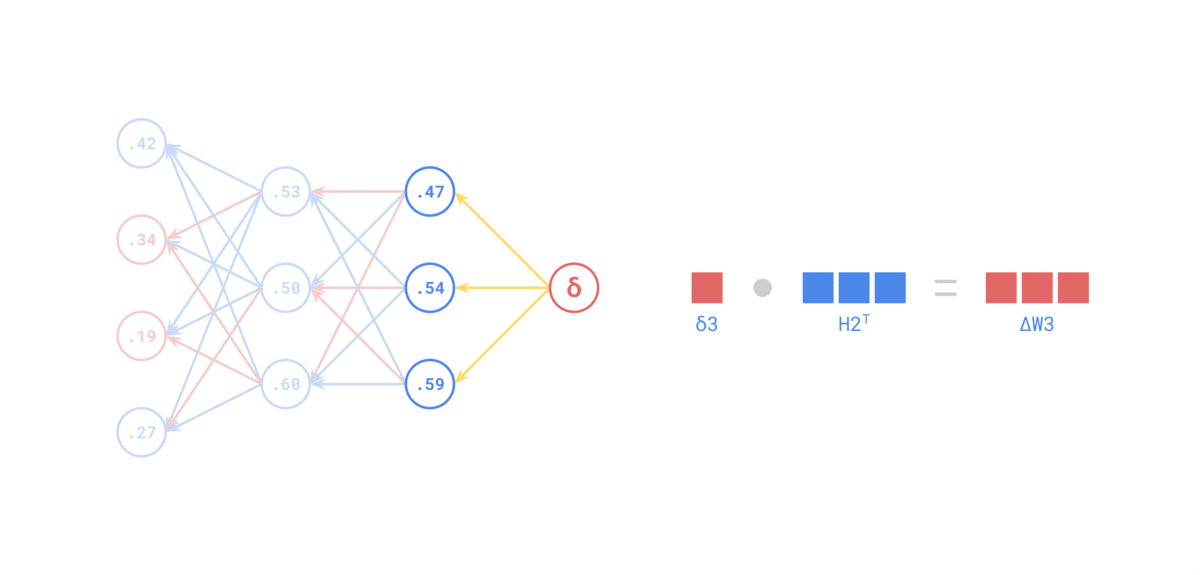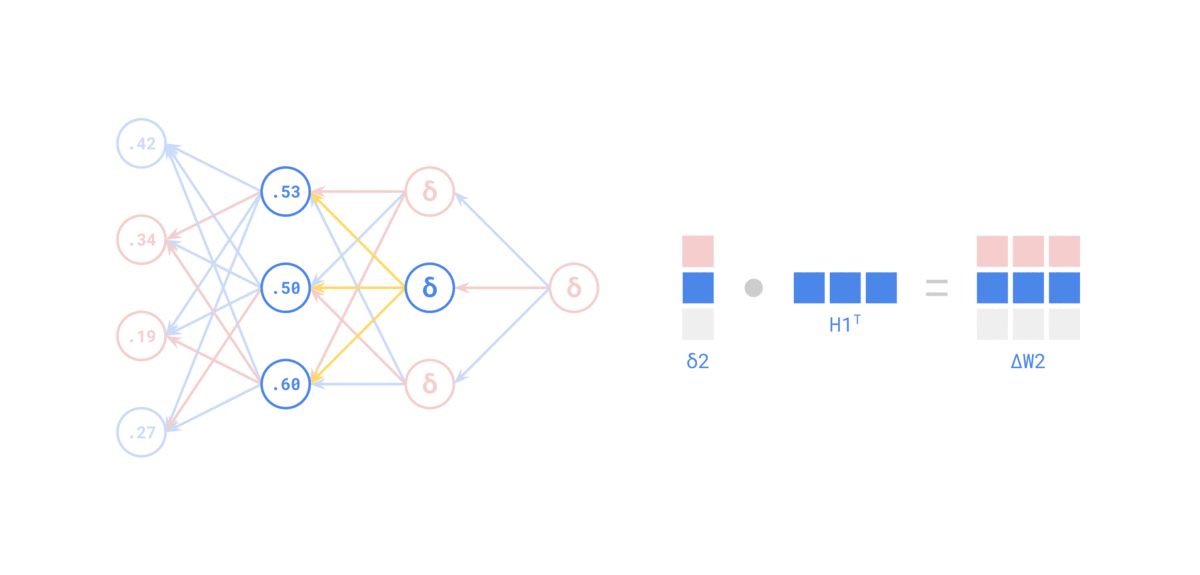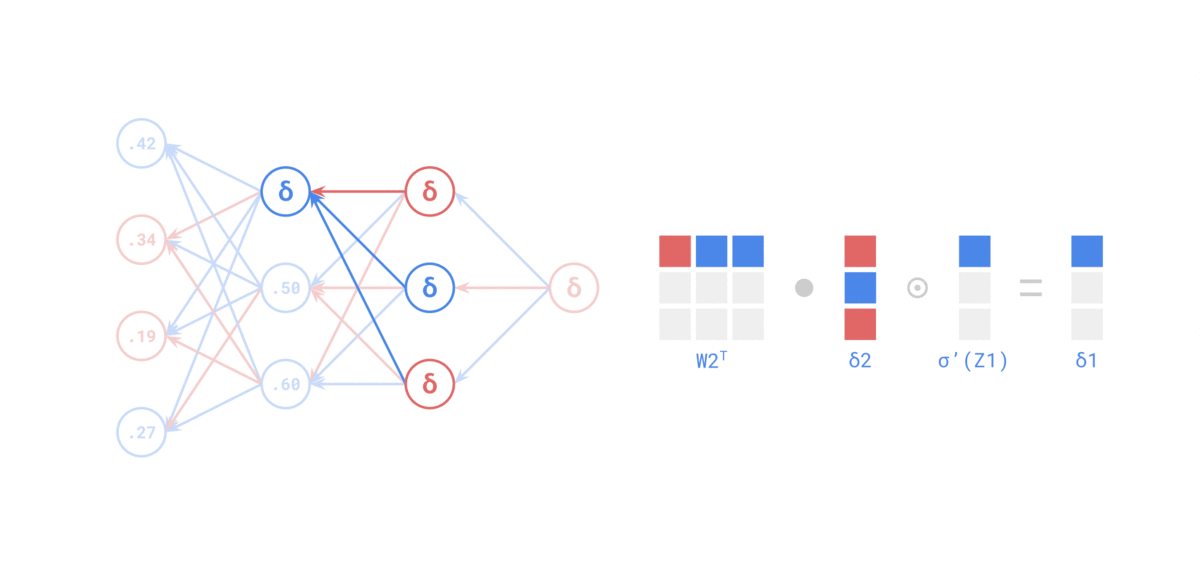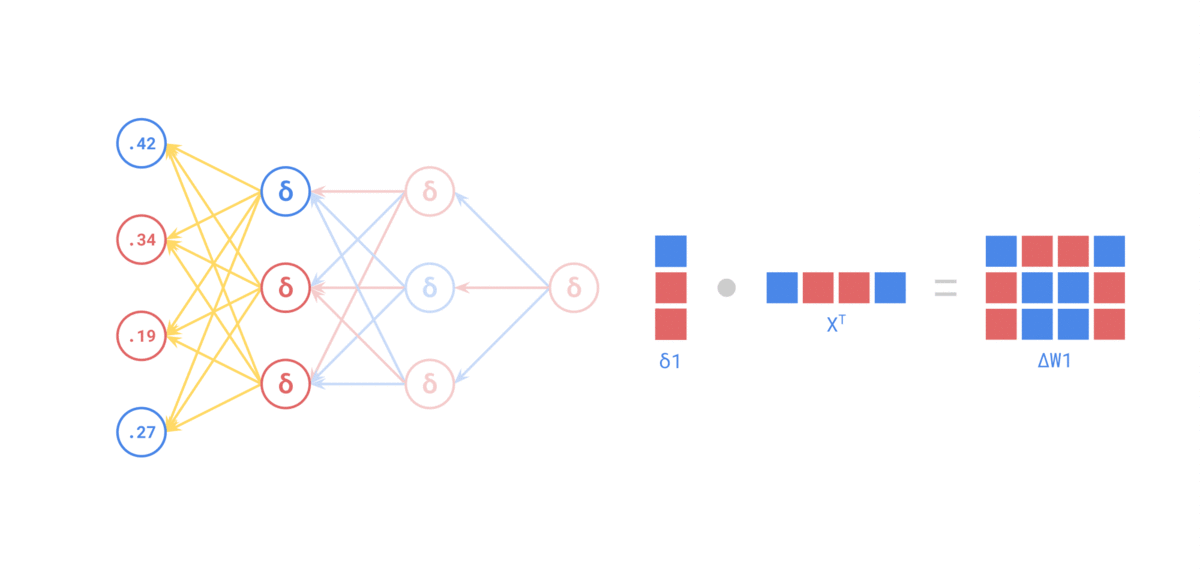
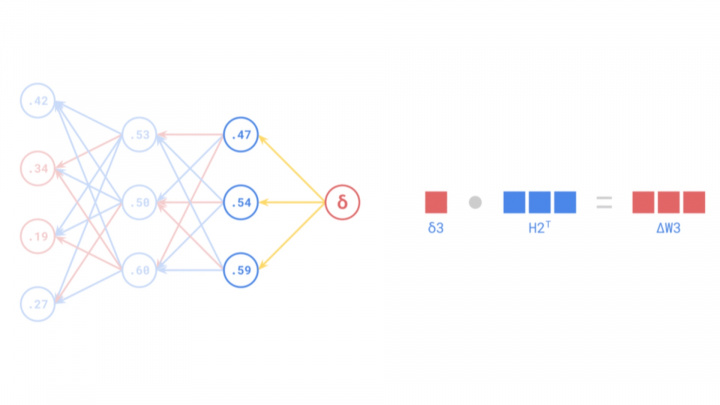
Source: https://medium.com/the-feynman-journal/what-makes-backpropagation-so-elegant-657f3afbbd

Formalisation et popularisation

La forme moderne et efficace de l'algorithme, connue sous le nom de différentiation automatique en mode inverse, a été rigoureusement décrite par le chercheur finlandais Seppo Linnainmaa dans sa thèse de master de 1970 (publiée en 1976). Linnainmaa a développé cette méthode générale pour calculer efficacement les dérivées de fonctions complexes et imbriquées, qui constitue aujourd'hui le cœur mathématique de la rétropropagation. Cependant, les travaux de Linnainmaa ne se sont pas concentrés sur les réseaux neuronaux.

Le lien crucial avec les réseaux neuronaux a été explicitement établi par Paul Werbos dans sa thèse de doctorat de 1974 (publiée ultérieurement). Werbos a reconnu que la différentiation automatique en mode inverse de Linnainmaa pouvait être appliquée à l'entraînement de réseaux neuronaux artificiels multicouches. Il a d'abord démontré comment cet algorithme pouvait ajuster efficacement les poids dans les perceptrons multicouches (PMC), surmontant ainsi les limitations des perceptrons monocouches et permettant aux réseaux d'apprendre des motifs complexes. Les travaux de Werbos ont constitué une avancée décisive dans le domaine de l'IA, ouvrant la voie aux progrès futurs des réseaux neuronaux.

Malgré ces développements, l'algorithme de rétropropagation n'a attiré l'attention générale qu'au milieu des années 1980. En 1986, David E. Rumelhart, Geoffrey Hinton et Ronald J. Williams ont publié leur article fondateur, "Learning representations by back-propagating errors." Cet article a clairement démontré la puissance pratique de la rétropropagation pour l'entraînement des PMC sur divers problèmes. L'étude a été d'une importance capitale car elle a montré de manière convaincante que les RNA pouvaient apprendre des représentations internes utiles et résoudre des tâches complexes que l'on pensait auparavant insolubles pour eux. L'article a joué un rôle clé non seulement dans la popularisation de l'algorithme, mais aussi dans la revitalisation de la recherche sur les réseaux neuronaux, qui avait été confrontée au scepticisme pendant le précédent "hiver de l'IA".

Cet article phare a ravivé l'intérêt pour les RNA au sein de la communauté de recherche en IA. Grâce à l'efficacité de la rétropropagation, les réseaux multicouches sont devenus effectivement entraînables, ouvrant la porte à la révolution de l'apprentissage profond et aux avancées majeures de l'intelligence artificielle moderne.

Source: https://medium.com/the-feynman-journal/what-makes-backpropagation-so-elegant-657f3afbbd

Applications pratiques : la percée de Yann LeCun

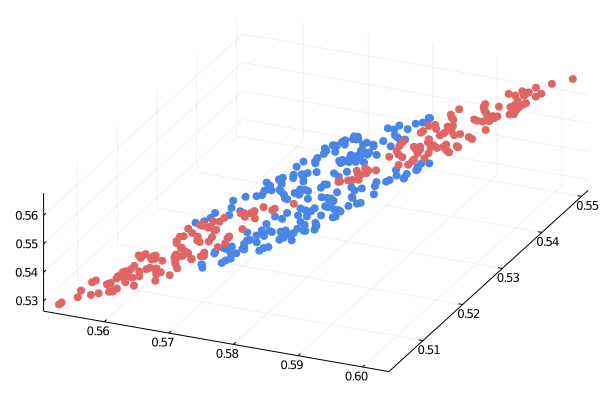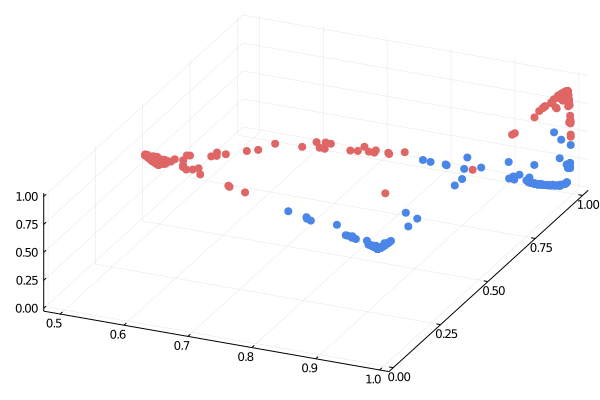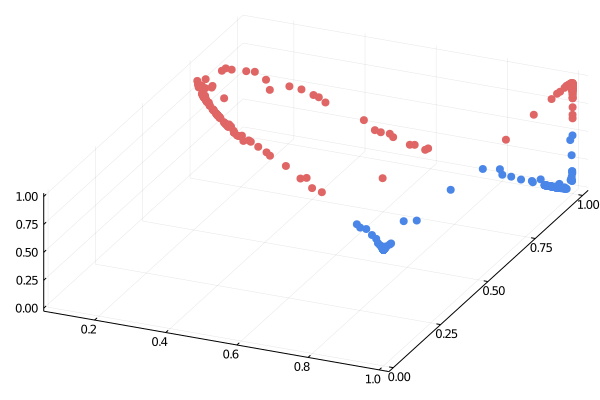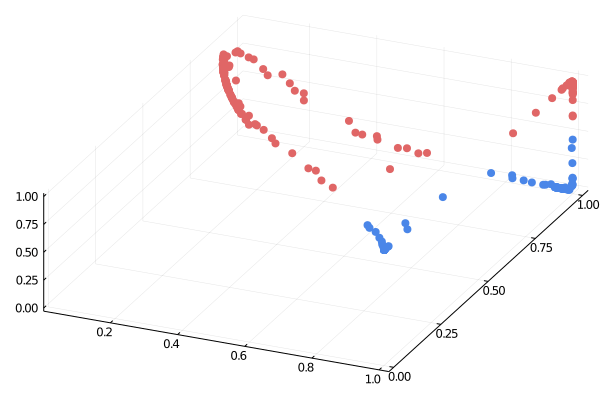
Bien que les bases théoriques de la rétropropagation aient été posées dans les années 1960 et 1970, sa première application pratique véritablement marquante a émergé à la fin des années 1980. Yann LeCun, aujourd'hui reconnu comme l'un des pionniers de l'IA, a démontré la puissance de la combinaison de la rétropropagation avec les réseaux neuronaux convolutionnels (CNN) alors qu'il travaillait aux Bell Labs en 1989. LeCun et ses collègues ont appliqué les CNN entraînés avec la rétropropagation à la tâche de la reconnaissance de chiffres manuscrits.

Cette application révolutionnaire a conduit au développement d'un système capable de lire automatiquement les chiffres manuscrits sur les chèques. Les travaux de LeCun ont non seulement prouvé que la rétropropagation pouvait résoudre des problèmes complexes du monde réel, mais ont également montré que les réseaux neuronaux, en particulier les architectures CNN, étaient très efficaces pour les tâches de vision par ordinateur. Cette percée a marqué le début d'une nouvelle ère dans l'IA, ouvrant la voie à l'utilisation généralisée des réseaux neuronaux et de la rétropropagation dans de nombreuses applications industrielles et de recherche.

Les travaux de LeCun ont été particulièrement importants car les CNN sont bien adaptés au traitement des données visuelles, car ils peuvent saisir les hiérarchies spatiales dans les images. La rétropropagation a permis à ces réseaux d'apprendre les poids de filtre appropriés pour minimiser les erreurs de classification, permettant une extraction efficace des caractéristiques significatives des données d'image.

Le nom de Yann LeCun est depuis devenu synonyme de CNN et d'apprentissage profond. En 2018, il a reçu, avec Geoffrey Hinton et Yoshua Bengio, le prix Turing, la plus haute distinction en informatique, pour leurs contributions fondamentales à l'apprentissage profond. Les travaux de LeCun ont fourni un pont crucial entre la théorie de la rétropropagation et de puissantes applications pratiques, ouvrant de nouveaux horizons pour l'intelligence artificielle.

Source: https://medium.com/the-feynman-journal/what-makes-backpropagation-so-elegant-657f3afbbd

Défis et évolution de la rétropropagation

Malgré son adoption généralisée et son utilité avérée, la rétropropagation n'était pas sans défis, en particulier lorsque les chercheurs ont commencé à construire des réseaux plus profonds. Deux problèmes importants ont émergé : les problèmes de disparition du gradient et d'explosion du gradient.

Le problème de la disparition du gradient

La disparition des gradients se produit dans les réseaux profonds lorsque le signal d'erreur diminue de façon exponentielle lorsqu'il se propage vers l'arrière de la couche de sortie vers les couches précédentes. Pendant la rétropropagation, les gradients sont calculés à l'aide de la règle de la chaîne, qui implique la multiplication de nombreux petits nombres (dérivées des fonctions d'activation, souvent inférieures à 1). Dans les réseaux profonds, cette multiplication répétée peut faire en sorte que le gradient devienne extrêmement petit, "disparaissant" effectivement. Par conséquent, les poids des couches précédentes ne se mettent pas à jour de manière significative, ce qui entrave le processus d'apprentissage. Cela a constitué un obstacle majeur à l'entraînement de réseaux neuronaux très profonds.

Le problème de l'explosion du gradient

Inversement, l'explosion des gradients se produit lorsque les gradients augmentent de façon exponentielle pendant la rétropropagation. Cela peut se produire si les poids ou les dérivées sont importants, ce qui entraîne des mises à jour massives des poids. Les poids du réseau peuvent rapidement diverger vers des valeurs extrêmes (comme NaN - Not a Number), ce qui provoque une instabilité et rend le réseau incapable d'apprendre.

Solutions et améliorations

Au fil des ans, les chercheurs ont développé de nombreuses techniques pour atténuer ces problèmes de gradient. Les principales solutions comprennent :

• Meilleures fonctions d'activation : Le remplacement de sigmoïde/tanh par des fonctions comme ReLU (Rectified Linear Unit) a contribué à atténuer la disparition des gradients, car la dérivée de ReLU est de 1 pour les entrées positives.
• Schémas d'initialisation des poids : Une initialisation prudente des poids (par exemple, l'initialisation Xavier/Glorot ou He) permet de maintenir les gradients dans une plage raisonnable.
• Normalisation par lots : Cette technique normalise les activations dans les couches intermédiaires, ce qui stabilise le réseau et permet des taux d'apprentissage plus élevés, ce qui contribue indirectement à résoudre les problèmes de gradient.
• Connexions résiduelles (ResNets) : Introduites dans les réseaux résiduels, ces "connexions sautées" permettent aux gradients de circuler plus facilement à travers le réseau en contournant certaines couches, ce qui combat efficacement le problème de la disparition du gradient dans les architectures très profondes.
• Écrêtage des gradients : Une technique simple pour prévenir l'explosion des gradients en plafonnant les valeurs des gradients s'ils dépassent un certain seuil.
• Algorithmes d'optimisation avancés : Les optimiseurs comme Adam, RMSProp et AdaGrad adaptent le taux d'apprentissage pour chaque paramètre, ce qui conduit souvent à une convergence plus rapide et à une meilleure gestion des paysages de gradients difficiles par rapport à la descente de gradient stochastique (SGD) standard.

Le rôle de la rétropropagation aujourd'hui

La rétropropagation reste l'un des algorithmes les plus cruciaux dans le domaine de l'apprentissage profond. Bien que de nombreuses variations et approches alternatives aient émergé, la rétropropagation (sous ses diverses formes, souvent combinée aux techniques ci-dessus) est toujours le cheval de bataille pour l'entraînement de la grande majorité des réseaux neuronaux. Les RNA modernes ont évolué vers des modèles extrêmement complexes capables de s'attaquer à certains des problèmes les plus difficiles de l'IA, notamment la vision par ordinateur, le traitement du langage naturel (NLP) et la conduite autonome. L'algorithme de rétropropagation a permis le développement de ces technologies avancées et continue d'être un pilier fondamental de l'apprentissage automatique.