Развитие алгоритма обратного распространения ошибки

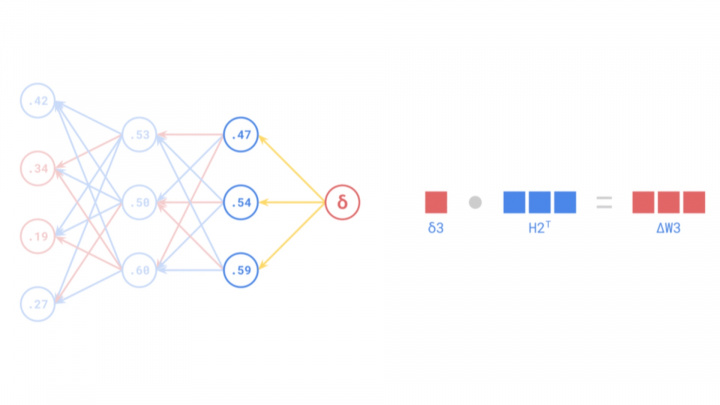
Хотя обратное распространение ошибки является незаменимым инструментом в современном искусственном интеллекте и машинном обучении, его история насчитывает несколько десятилетий и включает в себя множество научных прорывов. Его разработка началась концептуально в 1960-х годах, но широкое распространение он получил только в середине 1980-х годов после основополагающих работ и популяризации такими исследователями, как Фрэнк Розенблатт, Сеппо Линнайнмаа и Пол Вербос.

Ранние теоретические основы

Теоретические основы обратного распространения ошибки возникли еще в 1960-х годах благодаря работам различных исследователей в разных областях. Одним из ранних, концептуально связанных вкладов был вклад Фрэнка Розенблатта, известного разработкой Перцептрона, простой модели нейронной сети. В 1962 году он описал процедуру «обратного распространения коррекции ошибок» для своих идей многослойного перцептрона. Хотя однослойный перцептрон имел ограничения (известные своей неспособностью решить проблему XOR), и его конкретная коррекция ошибок не была общим обратным распространением ошибки, которое мы используем сегодня, работа Розенблатта заложила основу для дальнейших разработок в многослойных сетях.

Одновременно, в области теории управления и оптимизации, исследователи разрабатывали методы, основанные на цепном правиле для вычисления градиентов. Генри Дж. Келли в 1960 году предложил метод, в котором градиенты распространялись в обратном направлении через вычислительный граф, представляющий процесс управления. Стюарт Дрейфус опубликовал более простой вывод, основанный на цепном правиле, в 1962 году. Хотя в то время эти принципы эффективного вычисления производных путем обратного распространения информации не применялись непосредственно к нейронным сетям, они были важными предшественниками современного обратного распространения ошибки.

Однако в 1960-х годах область нейронных сетей все еще находилась в зачаточном состоянии, и вычислительных ресурсов, необходимых для эффективной реализации сложных алгоритмов, не хватало. Тем не менее, исследователи в области теории управления и оптимизации продолжали совершенствовать эти принципы, что в конечном итоге привело к современной форме алгоритма обратного распространения ошибки.

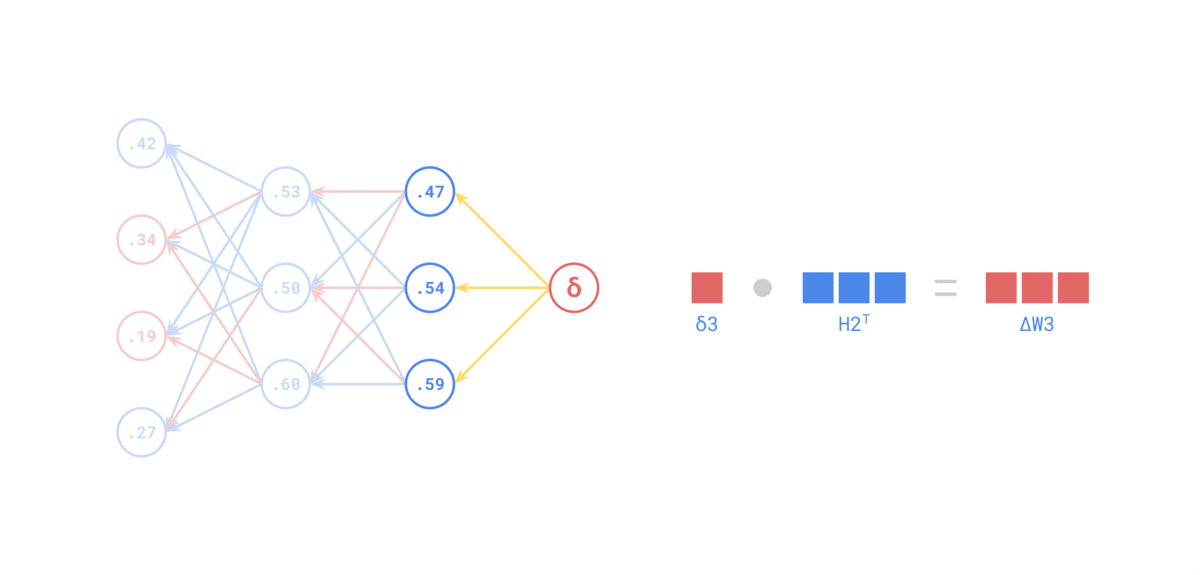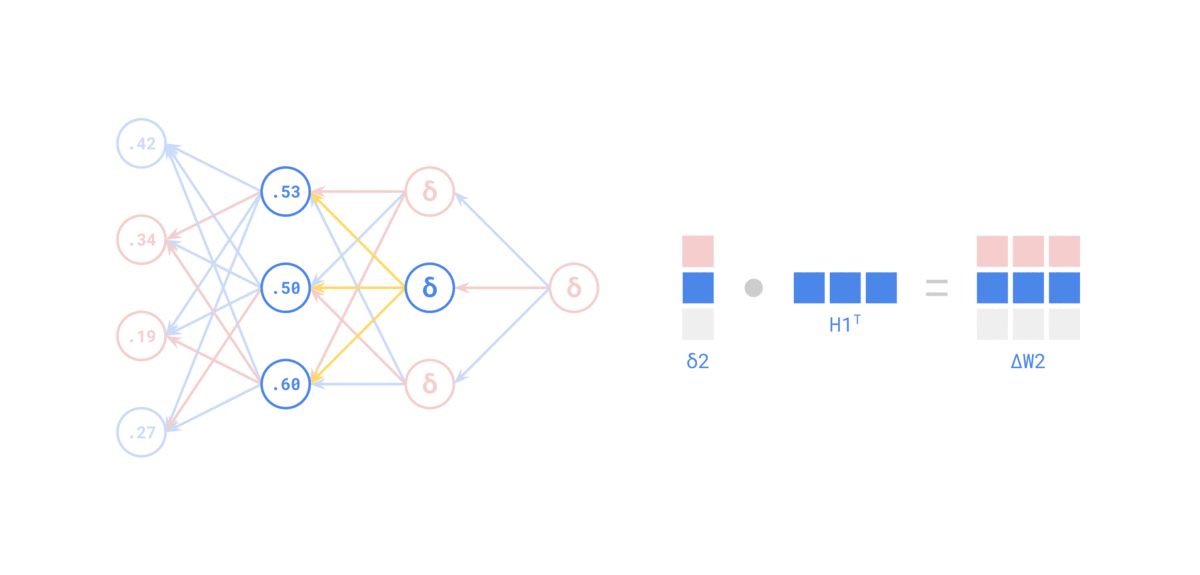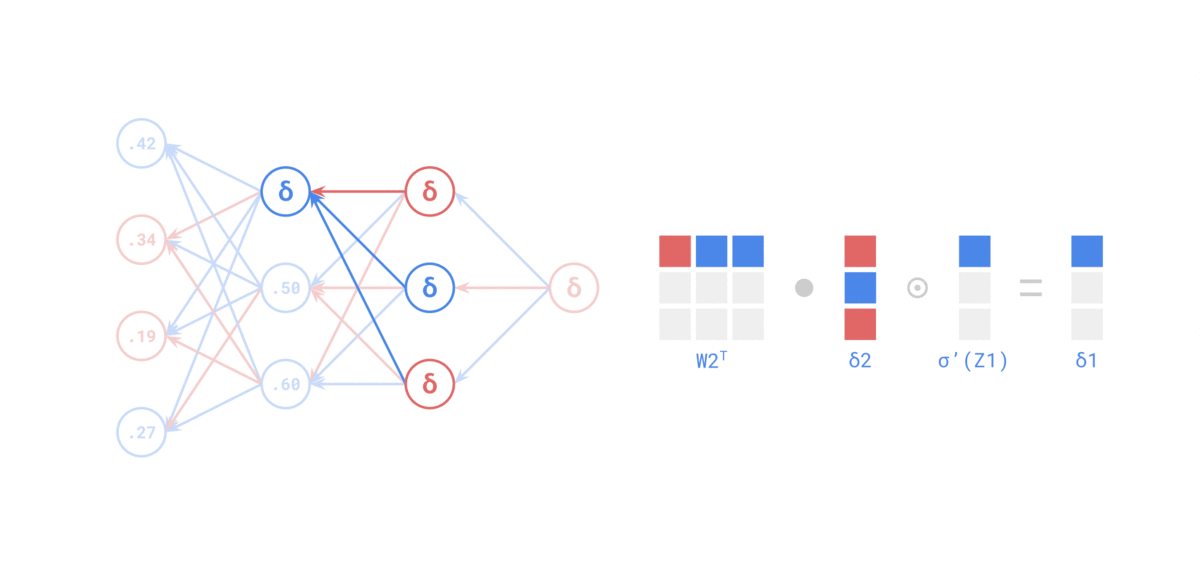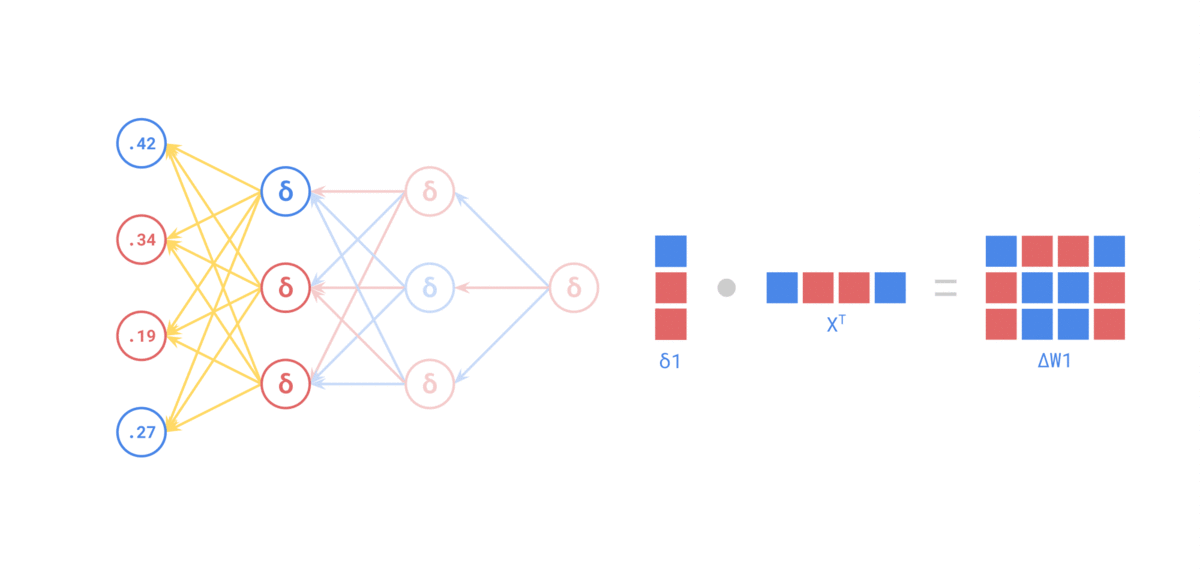
Источник: https://medium.com/the-feynman-journal/what-makes-backpropagation-so-elegant-657f3afbbd

Формализация и популяризация

Современная, эффективная форма алгоритма, известная как обратное автоматическое дифференцирование, была строго описана финским исследователем Сеппо Линнайнмаа в его магистерской диссертации 1970 года (опубликована в 1976 году). Линнайнмаа разработал этот общий метод для эффективного вычисления производных сложных, вложенных функций, который сегодня составляет математическую основу обратного распространения ошибки. Однако работа Линнайнмаа не была сосредоточена на нейронных сетях.

Ключевая связь с нейронными сетями была явно установлена Полом Вербосом в его докторской диссертации 1974 года (опубликована позже). Вербос признал, что обратное автоматическое дифференцирование Линнайнмаа можно применять для обучения многослойных искусственных нейронных сетей. Он первым продемонстрировал, как этот алгоритм может эффективно корректировать веса в многослойных перцептронах (МЛП), преодолевая ограничения однослойных перцептронов и позволяя сетям изучать сложные закономерности. Работа Вербоса стала прорывом в области ИИ, проложив путь для будущих достижений в нейронных сетях.

Несмотря на эти разработки, алгоритм обратного распространения ошибки получил широкое внимание только в середине 1980-х годов. В 1986 году Дэвид Э. Румельхарт, Джеффри Хинтон и Рональд Дж. Уильямс опубликовали свою основополагающую статью «Обучение представлений путем обратного распространения ошибок». В этой статье наглядно продемонстрирована практическая сила обратного распространения ошибки для обучения МЛП на различных задачах. Исследование было критически важным, потому что оно убедительно показало, что ИНС могут изучать полезные внутренние представления и решать сложные задачи, которые ранее считались для них неразрешимыми. Статья сыграла ключевую роль не только в популяризации алгоритма, но и в оживлении исследований в области нейронных сетей, которые столкнулись со скептицизмом во время предшествовавшей «зимы ИИ».

Эта знаковая статья вновь разожгла интерес к ИНС в исследовательском сообществе ИИ. Благодаря эффективности обратного распространения ошибки многослойные сети стали эффективно обучаемыми, открыв дверь революции глубокого обучения и крупным прорывам в современном искусственном интеллекте.

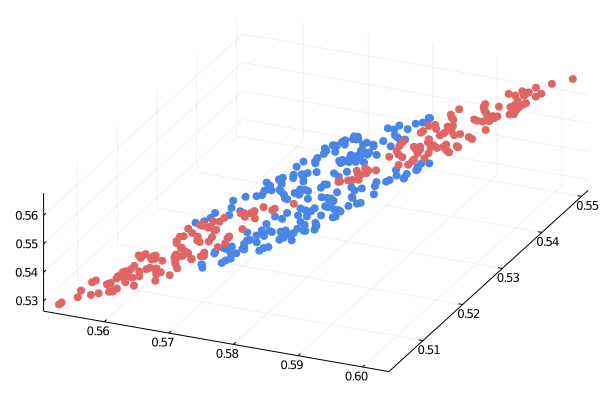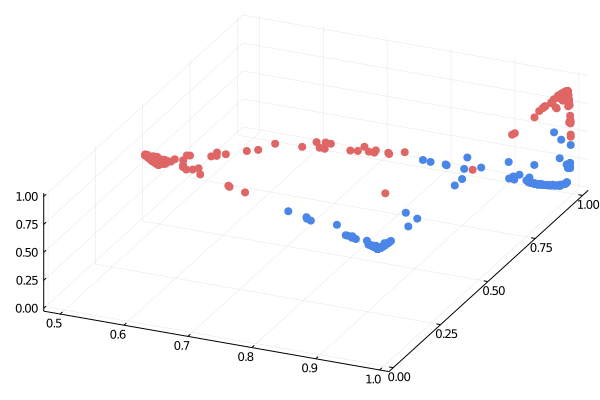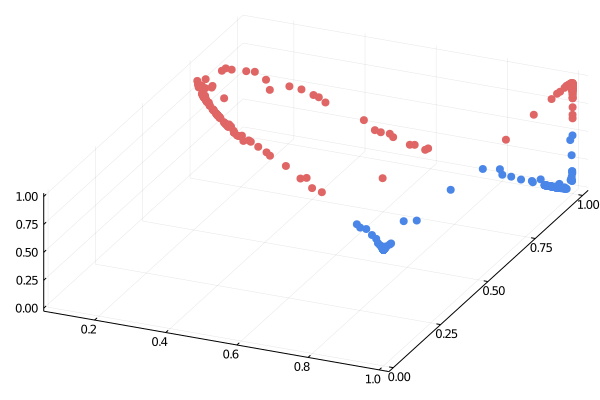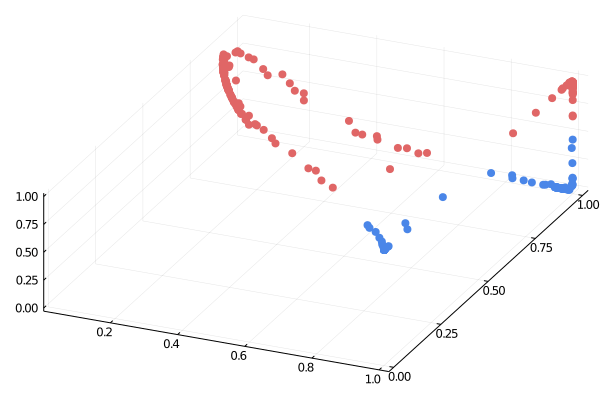
Источник: https://medium.com/the-feynman-journal/what-makes-backpropagation-so-elegant-657f3afbbd

Практическое применение: прорыв Янна ЛеКуна

Хотя теоретические основы обратного распространения ошибки были заложены в 1960-х и 1970-х годах, его первое по-настоящему значимое практическое применение появилось в конце 1980-х годов. Янн ЛеКун, которого сейчас признают одним из пионеров ИИ, продемонстрировал мощь сочетания обратного распространения ошибки со сверточными нейронными сетями (CNN), работая в Bell Labs в 1989 году. ЛеКун и его коллеги применили CNN, обученные с помощью обратного распространения ошибки, к задаче распознавания рукописных цифр.

Это революционное применение привело к разработке системы, способной автоматически считывать рукописные цифры на чеках. Работа ЛеКуна не только доказала, что обратное распространение ошибки может решать сложные, реальные задачи, но и показала, что нейронные сети, особенно архитектуры CNN, очень эффективны для задач компьютерного зрения. Этот прорыв ознаменовал начало новой эры в ИИ, проложив путь к широкому использованию нейронных сетей и обратного распространения ошибки в многочисленных промышленных и исследовательских приложениях.

Работа ЛеКуна была особенно значимой, поскольку CNN хорошо подходят для обработки визуальных данных, поскольку они могут улавливать пространственные иерархии в изображениях. Обратное распространение ошибки позволило этим сетям изучить соответствующие веса фильтров для минимизации ошибок классификации, обеспечивая эффективное извлечение значимых признаков из данных изображений.

Имя Янна ЛеКуна с тех пор стало синонимом CNN и глубокого обучения. В 2018 году он вместе с Джеффри Хинтоном и Йошуа Бенджио получил премию Тьюринга, высшую награду в области вычислительной техники, за их основополагающий вклад в глубокое обучение. Работа ЛеКуна обеспечила решающий мост от теории обратного распространения ошибки к мощным практическим приложениям, открыв новые горизонты для искусственного интеллекта.

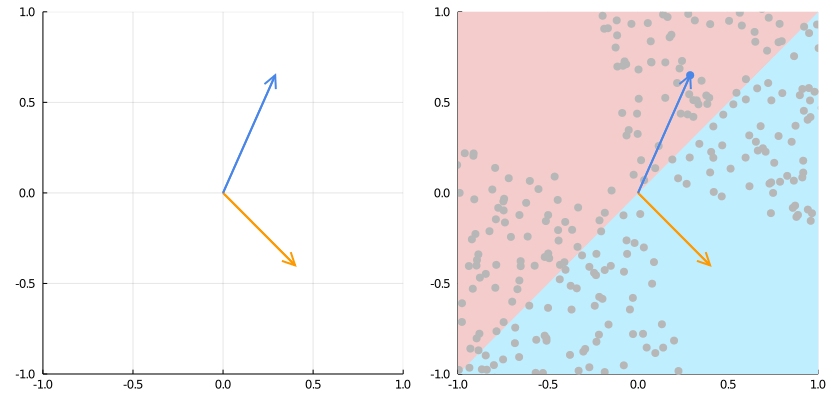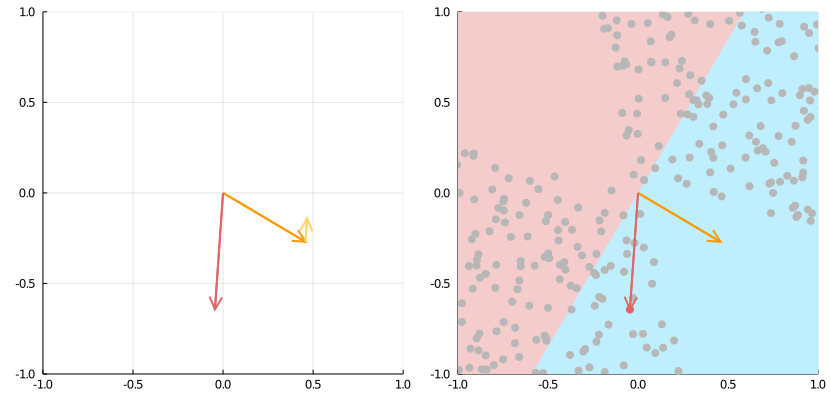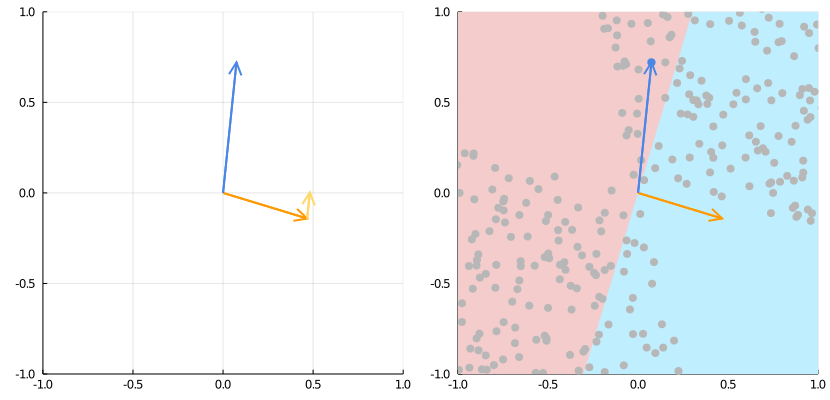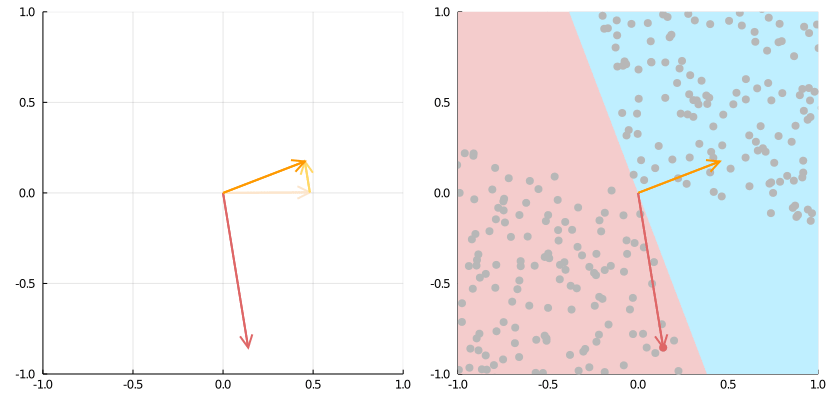
Источник: https://medium.com/the-feynman-journal/what-makes-backpropagation-so-elegant-657f3afbbd

Проблемы и эволюция обратного распространения ошибки

Несмотря на широкое распространение и доказанную полезность, обратное распространение ошибки не было лишено проблем, особенно когда исследователи начали строить более глубокие сети. Возникли две серьезные проблемы: проблема исчезающего градиента и проблема взрывающегося градиента.

Проблема исчезающего градиента

Исчезающие градиенты возникают в глубоких сетях, когда сигнал ошибки экспоненциально уменьшается по мере его распространения в обратном направлении от выходного слоя к более ранним слоям. Во время обратного распространения ошибки градиенты вычисляются с использованием цепного правила, которое включает умножение множества малых чисел (производных функций активации, часто меньше 1). В глубоких сетях это повторное умножение может привести к тому, что градиент станет чрезвычайно малым, фактически «исчезающим». В результате веса в более ранних слоях не обновляются значительно, что затрудняет процесс обучения. Это создало серьезное препятствие для обучения очень глубоких нейронных сетей.

Проблема взрывающегося градиента

И наоборот, взрывающиеся градиенты возникают, когда градиенты экспоненциально растут во время обратного распространения ошибки. Это может произойти, если веса или производные велики, что приводит к массовым обновлениям весов. Веса сети могут быстро разойтись до экстремальных значений (например, NaN - Not a Number), вызывая нестабильность и делая сеть неспособной к обучению.

Решения и улучшения

За прошедшие годы исследователи разработали множество методов для смягчения этих проблем с градиентами. Ключевые решения включают в себя:

• Улучшенные функции активации: Замена сигмоиды/tanh функциями, такими как ReLU (Rectified Linear Unit), помогла смягчить исчезающие градиенты, поскольку производная ReLU равна 1 для положительных входных данных.
• Схемы инициализации весов: Тщательная инициализация весов (например, инициализация Ксавье/Глоро или Хе) помогает удерживать градиенты в разумном диапазоне.
• Пакетная нормализация: Этот метод нормализует активации во внутренних слоях, стабилизируя сеть и позволяя использовать более высокие скорости обучения, что косвенно помогает в решении проблем с градиентами.
• Остаточные соединения (ResNets): Представленные в Residual Networks, эти «сквозные соединения» позволяют градиентам легче проходить через сеть, обходя некоторые слои, эффективно борясь с проблемой исчезающего градиента в очень глубоких архитектурах.
• Отсечение градиента: Простой метод предотвращения взрывающихся градиентов путем ограничения значений градиента, если они превышают определенный порог.
• Усовершенствованные алгоритмы оптимизации: Оптимизаторы, такие как Adam, RMSProp и AdaGrad, адаптируют скорость обучения для каждого параметра, что часто приводит к более быстрой сходимости и лучшему управлению сложными ландшафтами градиентов по сравнению со стандартным стохастическим градиентным спуском (SGD).

Роль обратного распространения ошибки сегодня

Обратное распространение ошибки остается одним из самых важных алгоритмов в области глубокого обучения. Хотя появилось множество вариаций и альтернативных подходов, обратное распространение ошибки (в различных его формах, часто в сочетании с вышеуказанными методами) по-прежнему является рабочей лошадкой для обучения подавляющего большинства нейронных сетей. Современные ИНС превратились в чрезвычайно сложные модели, способные решать одни из самых сложных задач в ИИ, включая компьютерное зрение, обработку естественного языка (NLP) и автономное вождение. Алгоритм обратного распространения ошибки позволил разработать эти передовые технологии и продолжает оставаться фундаментальной основой машинного обучения.