Die Entwicklung der Backpropagation

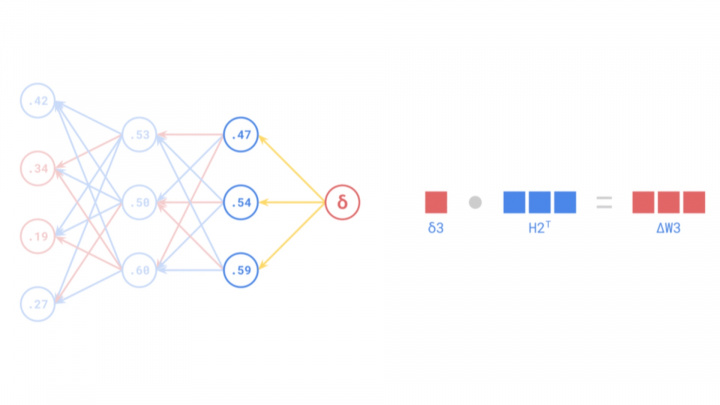
Obwohl die Backpropagation ein unverzichtbares Werkzeug in der modernen künstlichen Intelligenz und im maschinellen Lernen ist, reicht ihre Geschichte mehrere Jahrzehnte zurück und umfasst zahlreiche wissenschaftliche Durchbrüche. Ihre Entwicklung begann konzeptionell in den 1960er Jahren, erlangte aber erst Mitte der 1980er Jahre breite Bekanntheit nach grundlegenden Beiträgen und Popularisierung durch Forscher wie Frank Rosenblatt, Seppo Linnainmaa und Paul Werbos.

Frühe theoretische Grundlagen

Die theoretischen Grundlagen der Backpropagation entstanden bereits in den 1960er Jahren durch die Arbeit verschiedener Forscher in unterschiedlichen Bereichen. Ein früher, konzeptionell verwandter Beitrag kam von Frank Rosenblatt, der für die Entwicklung des Perceptron bekannt ist, einem einfachen Modell eines neuronalen Netzes. 1962 beschrieb er ein "Back-Propagating Error Correction"-Verfahren für seine mehrschichtigen Perceptron-Ideen. Während das einschichtige Perceptron Einschränkungen hatte (bekanntermaßen unfähig, das XOR-Problem zu lösen) und seine spezifische Fehlerkorrektur nicht die allgemeine Backpropagation war, die wir heute verwenden, legte Rosenblatts Arbeit den Grundstein für spätere Entwicklungen in mehrschichtigen Netzen.

Gleichzeitig entwickelten Forscher auf dem Gebiet der Steuerungstheorie und Optimierung Methoden, die auf der Kettenregel zur Berechnung von Gradienten basieren. Henry J. Kelley schlug 1960 eine Methode vor, bei der Gradienten rückwärts durch einen Berechnungsgraphen propagiert wurden, der einen Steuerungsprozess darstellte. Stuart Dreyfus veröffentlichte 1962 eine einfachere Ableitung, die auf der Kettenregel basiert. Obwohl diese Prinzipien der effizienten Berechnung von Ableitungen durch Rückwärtsleitung von Informationen zu dieser Zeit nicht direkt auf neuronale Netze angewendet wurden, waren sie entscheidende Vorläufer der modernen Backpropagation.

In den 1960er Jahren steckte das Gebiet der neuronalen Netze jedoch noch in den Kinderschuhen, und es mangelte an den Rechenressourcen, die für die effektive Implementierung komplexer Algorithmen erforderlich waren. Dennoch verfeinerten Forscher in der Steuerungstheorie und Optimierung diese Prinzipien weiter, was schließlich zur modernen Form des Backpropagation-Algorithmus führte.

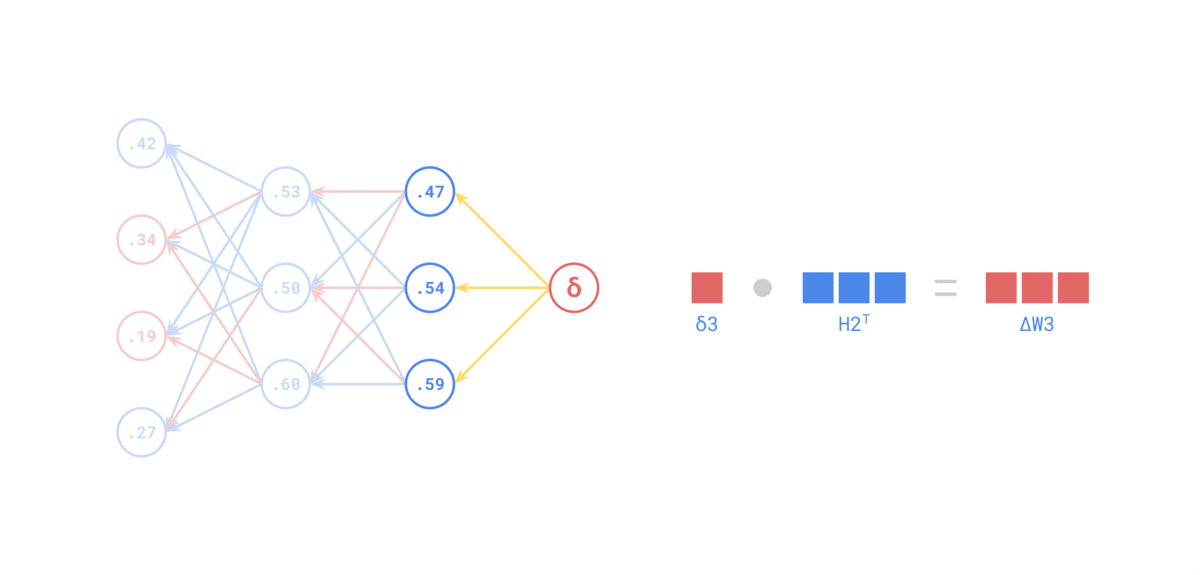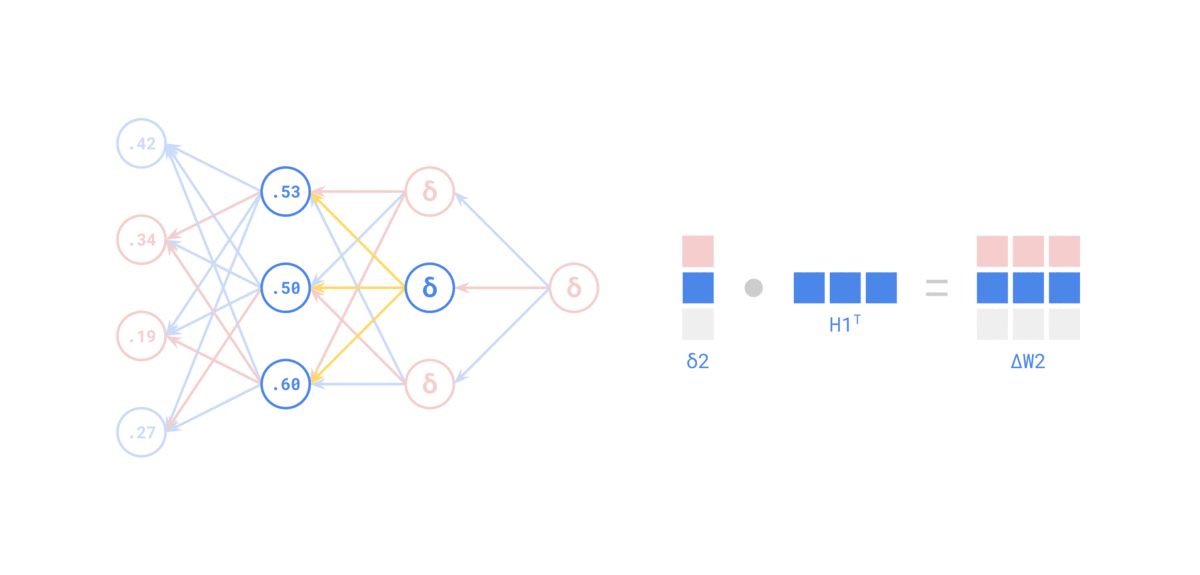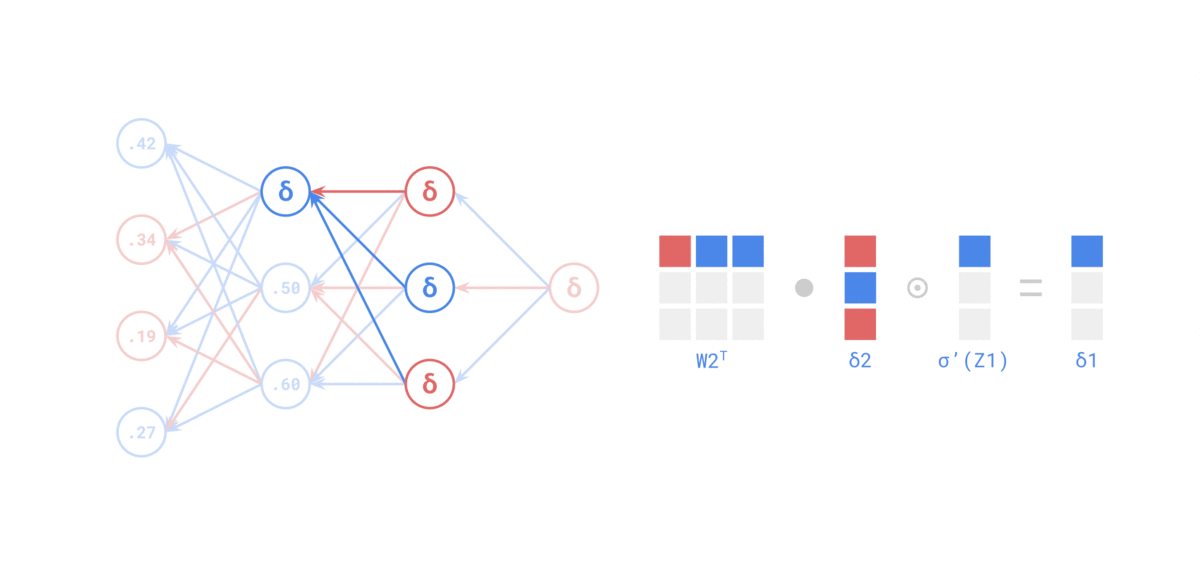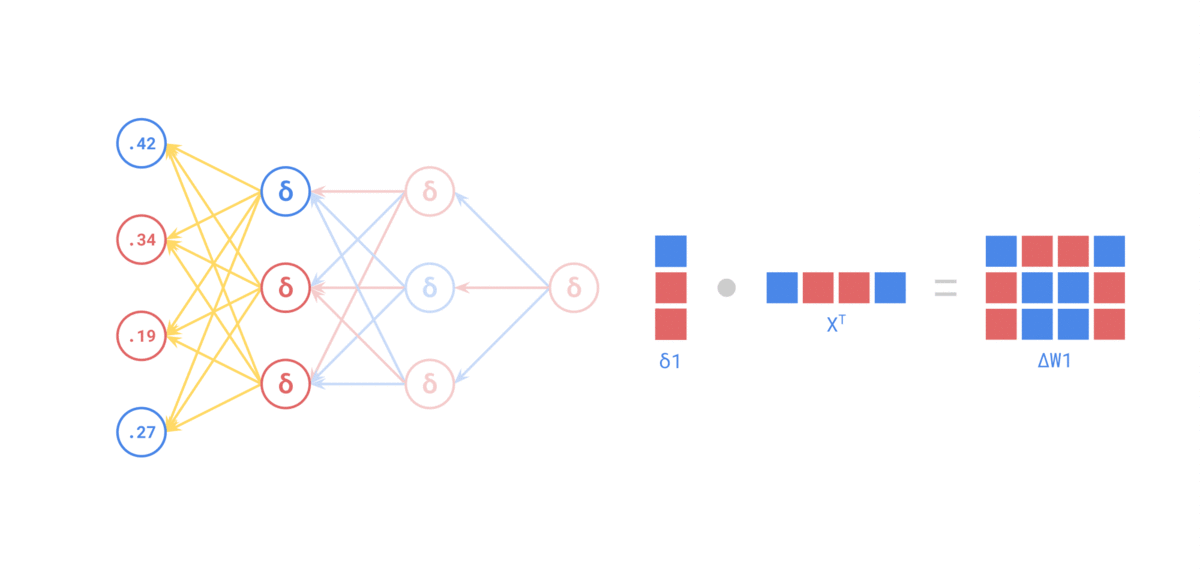
Quelle: https://medium.com/the-feynman-journal/what-makes-backpropagation-so-elegant-657f3afbbd

Formalisierung und Popularisierung

Die moderne, effiziente Form des Algorithmus, bekannt als Reverse-Mode Automatic Differentiation, wurde vom finnischen Forscher Seppo Linnainmaa in seiner Masterarbeit von 1970 (veröffentlicht 1976) rigoros beschrieben. Linnainmaa entwickelte diese allgemeine Methode zur effizienten Berechnung von Ableitungen komplexer, verschachtelter Funktionen, die heute den mathematischen Kern der Backpropagation bildet. Linnainmaas Arbeit konzentrierte sich jedoch nicht auf neuronale Netze.

Die entscheidende Verbindung zu neuronalen Netzen wurde von Paul Werbos in seiner Dissertation von 1974 (später veröffentlicht) explizit hergestellt. Werbos erkannte, dass Linnainmaas Reverse-Mode Automatic Differentiation zur Schulung mehrschichtiger künstlicher neuronaler Netze angewendet werden könnte. Er demonstrierte erstmals, wie dieser Algorithmus die Gewichte in mehrschichtigen Perceptrons (MLPs) effizient anpassen kann, wodurch die Einschränkungen einschichtiger Perceptrons überwunden und Netze in die Lage versetzt werden, komplexe Muster zu lernen. Werbos' Arbeit war ein Durchbruch auf dem Gebiet der KI und ebnete den Weg für zukünftige Fortschritte bei neuronalen Netzen.

Trotz dieser Entwicklungen erlangte der Backpropagation-Algorithmus erst Mitte der 1980er Jahre breite Aufmerksamkeit. 1986 veröffentlichten David E. Rumelhart, Geoffrey Hinton und Ronald J. Williams ihr bahnbrechendes Papier "Learning representations by back-propagating errors". Dieses Papier demonstrierte deutlich die praktische Leistungsfähigkeit der Backpropagation für das Training von MLPs bei verschiedenen Problemen. Die Studie war von entscheidender Bedeutung, da sie überzeugend zeigte, dass KNNs nützliche interne Darstellungen lernen und komplexe Aufgaben lösen können, die zuvor als für sie unlösbar galten. Das Papier spielte nicht nur eine Schlüsselrolle bei der Popularisierung des Algorithmus, sondern auch bei der Wiederbelebung der Forschung zu neuronalen Netzen, die während des vorangegangenen "KI-Winters" auf Skepsis gestoßen war.

Dieses bahnbrechende Papier entfachte das Interesse an KNNs innerhalb der KI-Forschungsgemeinschaft neu. Dank der Effizienz der Backpropagation wurden mehrschichtige Netze effektiv trainierbar, was die Tür zur Deep-Learning-Revolution und den großen Durchbrüchen in der modernen künstlichen Intelligenz öffnete.

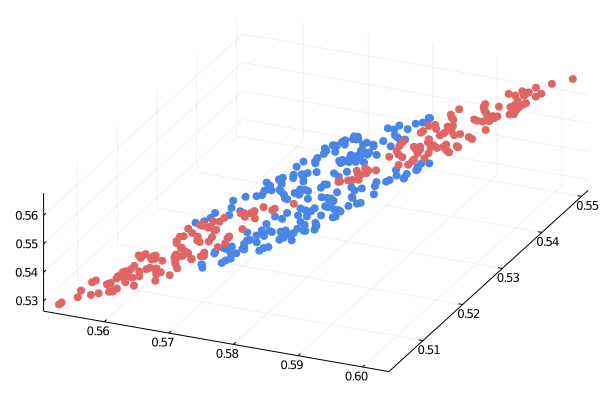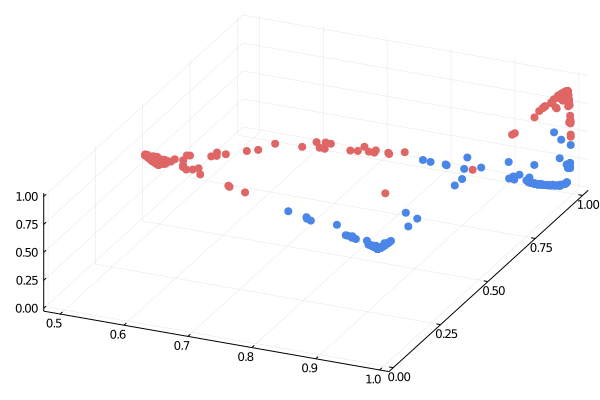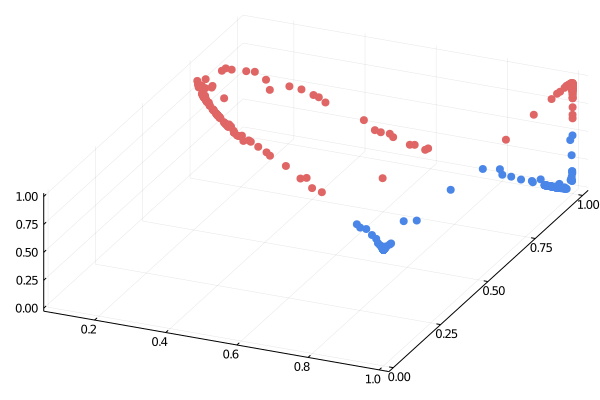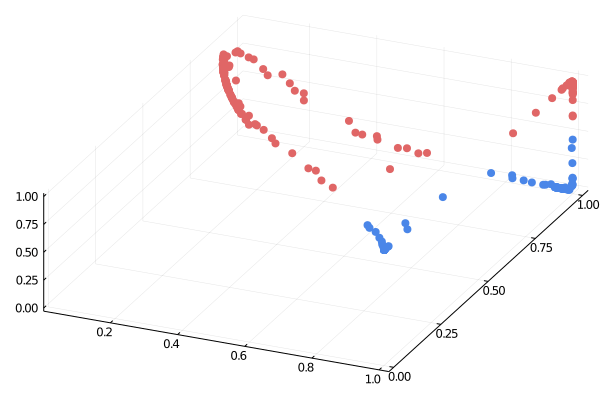
Quelle: https://medium.com/the-feynman-journal/what-makes-backpropagation-so-elegant-657f3afbbd

Praktische Anwendungen: Yann LeCuns Durchbruch

Obwohl die theoretischen Grundlagen der Backpropagation in den 1960er und 1970er Jahren gelegt wurden, entstand ihre erste wirklich wirkungsvolle praktische Anwendung in den späten 1980er Jahren. Yann LeCun, der heute als einer der Pioniere der KI gilt, demonstrierte die Leistungsfähigkeit der Kombination von Backpropagation mit Convolutional Neural Networks (CNNs), während er 1989 bei den Bell Labs arbeitete. LeCun und seine Kollegen wandten mit Backpropagation trainierte CNNs auf die Aufgabe der Handschriftenerkennung von Ziffern an.

Diese revolutionäre Anwendung führte zur Entwicklung eines Systems, das in der Lage ist, handgeschriebene Ziffern auf Schecks automatisch zu lesen. LeCuns Arbeit bewies nicht nur, dass Backpropagation komplexe, reale Probleme lösen kann, sondern zeigte auch, dass neuronale Netze, insbesondere CNN-Architekturen, für Computer-Vision-Aufgaben hochwirksam sind. Dieser Durchbruch markierte den Beginn einer neuen Ära in der KI und ebnete den Weg für den breiten Einsatz von neuronalen Netzen und Backpropagation in zahlreichen industriellen und Forschungsanwendungen.

LeCuns Arbeit war besonders bedeutsam, weil CNNs gut für die Verarbeitung visueller Daten geeignet sind, da sie die räumlichen Hierarchien in Bildern erfassen können. Backpropagation ermöglichte es diesen Netzen, die geeigneten Filtergewichte zu lernen, um Klassifizierungsfehler zu minimieren und eine effiziente Extraktion aussagekräftiger Merkmale aus Bilddaten zu ermöglichen.

Yann LeCuns Name ist seitdem ein Synonym für CNNs und Deep Learning. Im Jahr 2018 erhielt er zusammen mit Geoffrey Hinton und Yoshua Bengio den Turing Award, die höchste Auszeichnung der Informatik, für ihre grundlegenden Beiträge zum Deep Learning. LeCuns Arbeit schlug eine entscheidende Brücke von der Theorie der Backpropagation zu leistungsstarken praktischen Anwendungen und eröffnete neue Horizonte für die künstliche Intelligenz.

Quelle: https://medium.com/the-feynman-journal/what-makes-backpropagation-so-elegant-657f3afbbd

Herausforderungen und Weiterentwicklung der Backpropagation

Trotz ihrer breiten Akzeptanz und ihres nachgewiesenen Nutzens war die Backpropagation nicht ohne Herausforderungen, insbesondere als Forscher begannen, tiefere Netze zu bauen. Zwei bedeutende Probleme traten auf: das Problem des verschwindenden Gradienten und des explodierenden Gradienten.

Das Problem des verschwindenden Gradienten

Verschwindende Gradienten treten in tiefen Netzen auf, wenn das Fehlersignal exponentiell abnimmt, während es sich von der Ausgabeschicht zu den früheren Schichten rückwärts ausbreitet. Während der Backpropagation werden Gradienten mit der Kettenregel berechnet, bei der viele kleine Zahlen (Ableitungen von Aktivierungsfunktionen, oft kleiner als 1) multipliziert werden. In tiefen Netzen kann diese wiederholte Multiplikation dazu führen, dass der Gradient extrem klein wird und effektiv "verschwindet". Infolgedessen werden die Gewichte in den früheren Schichten nicht signifikant aktualisiert, was den Lernprozess behindert. Dies stellte ein großes Hindernis für das Training sehr tiefer neuronaler Netze dar.

Das Problem des explodierenden Gradienten

Umgekehrt treten explodierende Gradienten auf, wenn die Gradienten während der Backpropagation exponentiell groß werden. Dies kann passieren, wenn die Gewichte oder die Ableitungen groß sind, was zu massiven Aktualisierungen der Gewichte führt. Die Gewichte des Netzes können schnell auf extreme Werte (wie NaN - Not a Number) divergieren, was zu Instabilität führt und das Netz unfähig macht zu lernen.

Lösungen und Verbesserungen

Im Laufe der Jahre entwickelten Forscher zahlreiche Techniken, um diese Gradientenprobleme zu mildern. Zu den wichtigsten Lösungen gehören:

• Bessere Aktivierungsfunktionen: Der Ersatz von Sigmoid/Tanh durch Funktionen wie ReLU (Rectified Linear Unit) trug zur Linderung verschwindender Gradienten bei, da die Ableitung von ReLU für positive Eingaben 1 ist.
• Gewichtsinitialisierungsschemata: Eine sorgfältige Initialisierung der Gewichte (z. B. Xavier/Glorot- oder He-Initialisierung) trägt dazu bei, die Gradienten in einem vernünftigen Bereich zu halten.
• Batch-Normalisierung: Diese Technik normalisiert die Aktivierungen innerhalb von Zwischenschichten, stabilisiert das Netz und ermöglicht höhere Lernraten, was indirekt bei Gradientenproblemen hilft.
• Residuelle Verbindungen (ResNets): Diese in Residual Networks eingeführten "Skip-Verbindungen" ermöglichen es Gradienten, leichter durch das Netz zu fließen, indem sie einige Schichten umgehen, wodurch das Problem des verschwindenden Gradienten in sehr tiefen Architekturen effektiv bekämpft wird.
• Gradientenbeschneidung: Eine einfache Technik zur Verhinderung explodierender Gradienten durch Begrenzung der Gradientenwerte, wenn sie einen bestimmten Schwellenwert überschreiten.
• Fortschrittliche Optimierungsalgorithmen: Optimierer wie Adam, RMSProp und AdaGrad passen die Lernrate für jeden Parameter an, was im Vergleich zum Standard-Stochastic Gradient Descent (SGD) oft zu einer schnelleren Konvergenz und einem besseren Umgang mit schwierigen Gradientenlandschaften führt.

Die Rolle der Backpropagation heute

Backpropagation ist nach wie vor einer der wichtigsten Algorithmen auf dem Gebiet des Deep Learning. Obwohl zahlreiche Variationen und alternative Ansätze entstanden sind, ist Backpropagation (in ihren verschiedenen Formen, oft kombiniert mit den oben genannten Techniken) immer noch das Arbeitspferd für das Training der überwiegenden Mehrheit der neuronalen Netze. Moderne KNNs haben sich zu extrem komplexen Modellen entwickelt, die in der Lage sind, einige der größten Herausforderungen der KI zu bewältigen, darunter Computer Vision, natürliche Sprachverarbeitung (NLP) und autonomes Fahren. Der Backpropagation-Algorithmus ermöglichte die Entwicklung dieser fortschrittlichen Technologien und ist nach wie vor eine grundlegende Säule des maschinellen Lernens.