The Development of Backpropagation

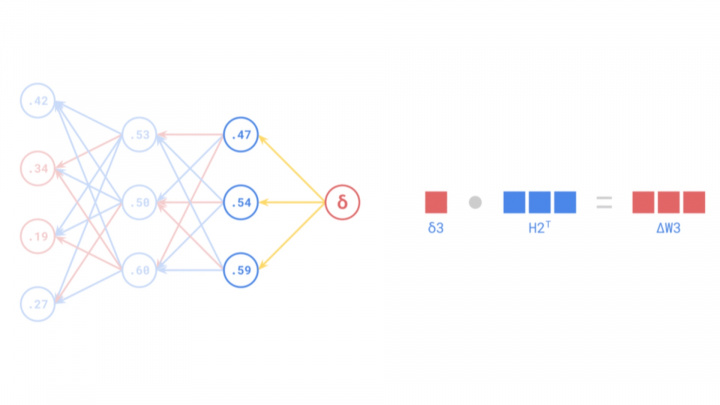
Although an indispensable tool in modern artificial intelligence and machine learning, the history of backpropagation spans several decades and involves numerous scientific breakthroughs. Its development began conceptually in the 1960s, but it only gained widespread prominence in the mid-1980s after foundational contributions and popularization by researchers such as Frank Rosenblatt, Seppo Linnainmaa, and Paul Werbos.

Early Theoretical Foundations

The theoretical underpinnings of backpropagation emerged as early as the 1960s through the work of various researchers across different fields. An early, conceptually related contribution came from Frank Rosenblatt, known for developing the Perceptron, a simple model of a neural network. In 1962, he described a "back-propagating error correction" procedure for his multi-layer perceptron ideas. While the single-layer perceptron had limitations (famously unable to solve the XOR problem), and his specific error correction wasn't the general backpropagation we use today, Rosenblatt's work laid groundwork for later developments in multi-layer networks.

Simultaneously, in the field of control theory and optimization, researchers were developing methods based on the chain rule for calculating gradients. Henry J. Kelley, in 1960, proposed a method where gradients were propagated backward through a computational graph representing a control process. Stuart Dreyfus published a simpler derivation based on the chain rule in 1962. While not directly applied to neural networks at the time, these principles of efficiently calculating derivatives by propagating information backward were crucial precursors to modern backpropagation.

However, in the 1960s, the field of neural networks was still nascent, and the computational resources required to implement complex algorithms effectively were lacking. Nevertheless, researchers in control theory and optimization continued to refine these principles, which eventually led to the modern form of the backpropagation algorithm.

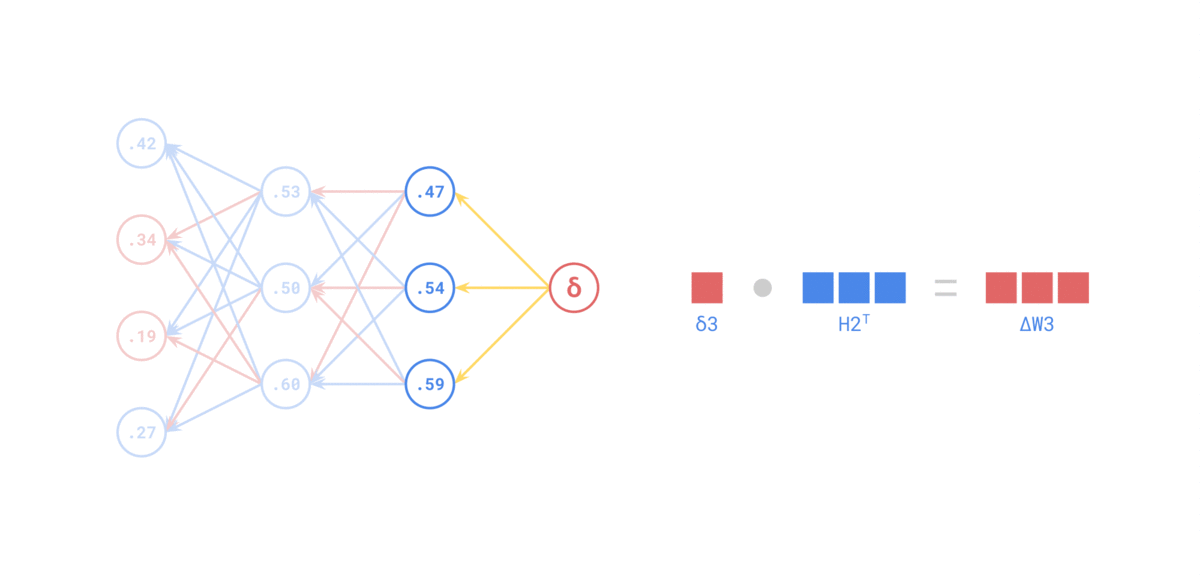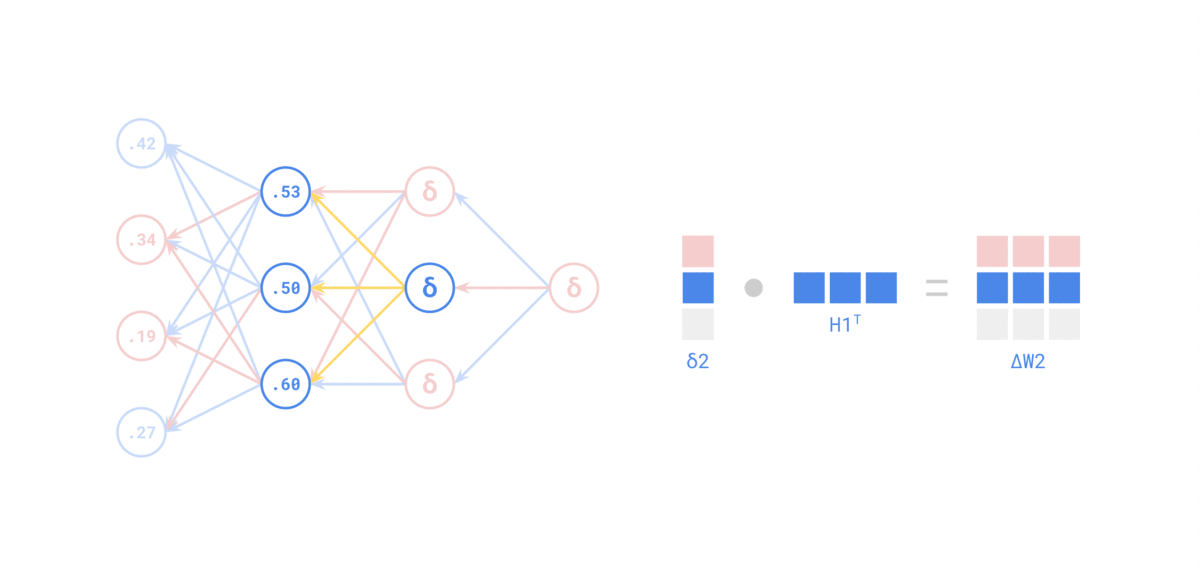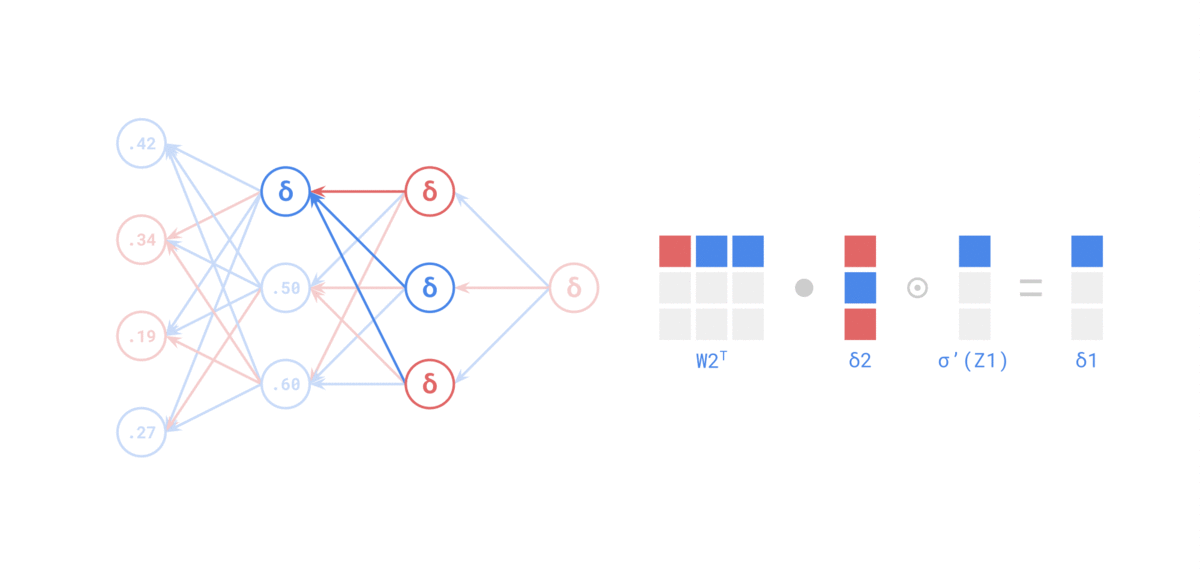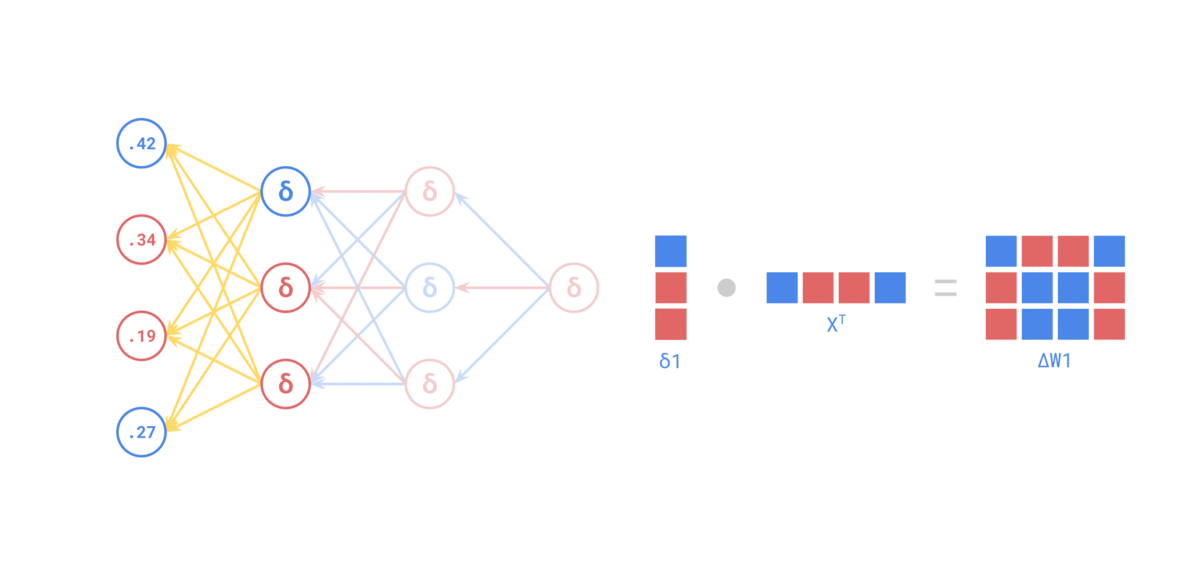
Source: https://medium.com/the-feynman-journal/what-makes-backpropagation-so-elegant-657f3afbbd

Formalization and Popularization

The modern, efficient form of the algorithm, known as **reverse-mode automatic differentiation**, was rigorously described by Finnish researcher Seppo Linnainmaa in his 1970 master's thesis (published 1976). Linnainmaa developed this general method for efficiently calculating derivatives of complex, nested functions, which forms the mathematical core of backpropagation today. However, Linnainmaa's work did not focus on neural networks.

The crucial connection to neural networks was made explicit by Paul Werbos in his 1974 Ph.D. thesis (published later). Werbos recognized that Linnainmaa's reverse-mode automatic differentiation could be applied to train multi-layer artificial neural networks. He first demonstrated how this algorithm could efficiently adjust the weights in multi-layer perceptrons (MLPs), overcoming the limitations of single-layer perceptrons and enabling networks to learn complex patterns. Werbos's work was a breakthrough in the AI field, paving the way for future advancements in neural networks.

Despite these developments, the backpropagation algorithm gained widespread attention only in the mid-1980s. In 1986, David E. Rumelhart, Geoffrey Hinton, and Ronald J. Williams published their seminal paper, "Learning representations by back-propagating errors." This paper clearly demonstrated the practical power of backpropagation for training MLPs on various problems. The study was critically important because it showed convincingly that ANNs could learn useful internal representations and solve complex tasks previously thought intractable for them. The paper played a key role not only in popularizing the algorithm but also in revitalizing research into neural networks, which had faced skepticism during the preceding "AI winter."

This landmark paper reignited interest in ANNs within the AI research community. Thanks to the efficiency of backpropagation, multi-layer networks became effectively trainable, opening the door to the deep learning revolution and the major breakthroughs in modern artificial intelligence.

Source: https://medium.com/the-feynman-journal/what-makes-backpropagation-so-elegant-657f3afbbd

Practical Applications: Yann LeCun's Breakthrough

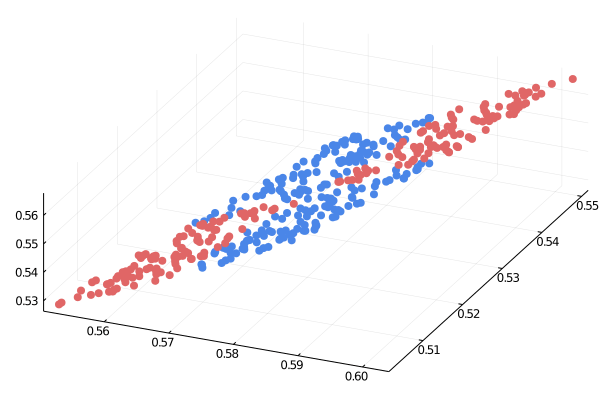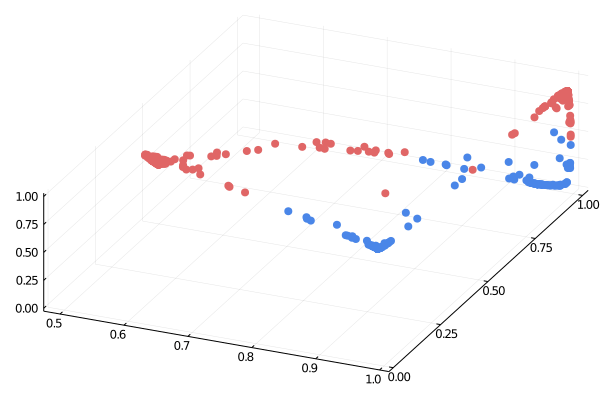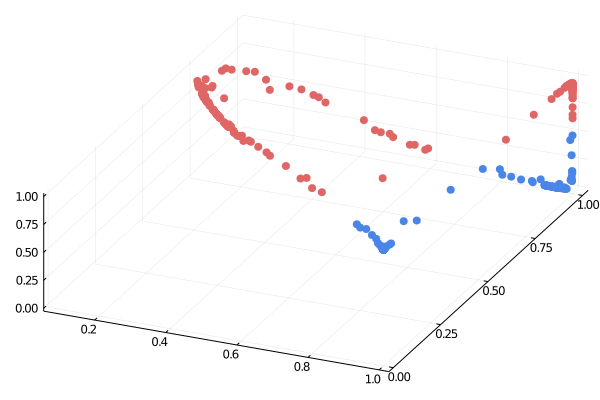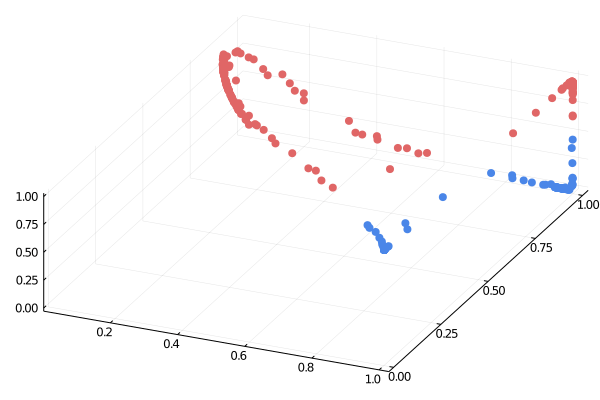
Although the theoretical foundations of backpropagation were laid in the 1960s and 1970s, its first truly impactful practical application emerged in the late 1980s. Yann LeCun, now recognized as one of the pioneers of AI, demonstrated the power of combining backpropagation with **Convolutional Neural Networks (CNNs)** while working at Bell Labs in 1989. LeCun and his colleagues applied CNNs trained with backpropagation to the task of **handwritten digit recognition**.

This revolutionary application led to the development of a system capable of automatically reading handwritten digits on checks. LeCun's work not only proved that backpropagation could solve complex, real-world problems but also showed that neural networks, particularly CNN architectures, were highly effective for computer vision tasks. This breakthrough marked the beginning of a new era in AI, paving the way for the widespread use of neural networks and backpropagation in numerous industrial and research applications.

LeCun's work was particularly significant because CNNs are well-suited for processing visual data, as they can capture the spatial hierarchies in images. Backpropagation allowed these networks to learn the appropriate filter weights to minimize classification errors, enabling efficient extraction of meaningful features from image data.

Yann LeCun's name has since become synonymous with CNNs and deep learning. In 2018, he, along with Geoffrey Hinton and Yoshua Bengio, received the **Turing Award**, computing's highest honor, for their foundational contributions to deep learning. LeCun's work provided a crucial bridge from the theory of backpropagation to powerful practical applications, opening new horizons for artificial intelligence.

Source: https://medium.com/the-feynman-journal/what-makes-backpropagation-so-elegant-657f3afbbd

Challenges and Evolution of Backpropagation

Despite its widespread adoption and proven utility, backpropagation was not without its challenges, especially as researchers began building deeper networks. Two significant problems emerged: the **vanishing gradient** and **exploding gradient** problems.

The Vanishing Gradient Problem

Vanishing gradients occur in deep networks when the error signal diminishes exponentially as it propagates backward from the output layer to the earlier layers. During backpropagation, gradients are calculated using the chain rule, which involves multiplying many small numbers (derivatives of activation functions, often less than 1). In deep networks, this repeated multiplication can cause the gradient to become extremely small, effectively "vanishing." As a result, the weights in the earlier layers do not update significantly, hindering the learning process. This posed a major obstacle to training very deep neural networks.

The Exploding Gradient Problem

Conversely, exploding gradients occur when the gradients grow exponentially large during backpropagation. This can happen if the weights or the derivatives are large, leading to massive updates to the weights. The network's weights can quickly diverge to extreme values (like NaN - Not a Number), causing instability and making the network unable to learn.

Solutions and Enhancements

Over the years, researchers developed numerous techniques to mitigate these gradient problems. Key solutions include:

• Better Activation Functions: Replacing sigmoid/tanh with functions like ReLU (Rectified Linear Unit) helped alleviate vanishing gradients as ReLU's derivative is 1 for positive inputs.
• Weight Initialization Schemes: Careful initialization of weights (e.g., Xavier/Glorot or He initialization) helps keep gradients in a reasonable range.
• Batch Normalization: This technique normalizes the activations within intermediate layers, stabilizing the network and allowing for higher learning rates, which indirectly helps with gradient issues.
• Residual Connections (ResNets): Introduced in Residual Networks, these "skip connections" allow gradients to flow more easily through the network by bypassing some layers, effectively combating the vanishing gradient problem in very deep architectures.
• Gradient Clipping: A simple technique to prevent exploding gradients by capping the gradient values if they exceed a certain threshold.
• Advanced Optimization Algorithms: Optimizers like Adam, RMSProp, and AdaGrad adapt the learning rate for each parameter, often leading to faster convergence and better handling of challenging gradient landscapes compared to standard stochastic gradient descent (SGD).

The Role of Backpropagation Today

Backpropagation remains one of the most crucial algorithms in the field of deep learning. Although numerous variations and alternative approaches have emerged, backpropagation (in its various forms, often combined with the techniques above) is still the workhorse for training the vast majority of neural networks. Modern ANNs have evolved into extremely complex models capable of tackling some of the most challenging problems in AI, including computer vision, natural language processing (NLP), and autonomous driving. The backpropagation algorithm enabled the development of these advanced technologies and continues to be a fundamental pillar of machine learning.